一、选择题 (本题共 10 小题, 每小题 5 分, 共 50 分. 在每小题给出的四个选项中, 只有一项符合题目 要求,把所选项前的字母填在题后的括号内. )
(1) 数一2021 函数 f ( x ) = { e x − 1 x , x ≠ 0 , 1 , x = 0 \displaystyle f(x)=\left\{\begin{array}{ll}\frac{\mathrm{e}^{x}-1}{x}, & x \neq 0, \\ 1, & x=0\end{array}\right. f ( x ) = { x e x − 1 , 1 , x = 0 , x = 0 x = 0 x=0 x = 0
(1) 数一2021 答 应选 D. 思路 这道题先使用导数的定义, 在连续使用两次洛必达求得求得极限 因为 f ′ ( 0 ) = 导数定义 lim x → 0 f ( x ) − f ( 0 ) x = f ( 0 ) = 1 f ( x ) = e x − 1 x lim x → 0 e x − 1 x − x x \displaystyle f'(0) \xlongequal[]{\text{导数定义}}\lim_{x \to 0} \frac{f(x) - f(0)}{x} \xlongequal[f(0)=1]{f(x)=\frac{e^{x}-1}{x}}\lim_{x \to 0} \frac{\frac{e^x - 1}{x} - x}{x} f ′ ( 0 ) 导数定义 x → 0 lim x f ( x ) − f ( 0 ) f ( x ) = x e x − 1 f ( 0 ) = 1 x → 0 lim x x e x − 1 − x = 通分 lim x → 0 e x − 1 − x x 2 = 或洛必达 泰勒 lim x → 0 1 2 x 2 = 1 2 \displaystyle \xlongequal[]{\text{通分}}\lim_{x \to 0} \frac{e^x - 1 - x}{x^2} \xlongequal[\text{或洛必达}]{\text{泰勒}}\lim_{x \to 0} \frac{1}{2}x^2 = \frac{1}{2} 通分 x → 0 lim x 2 e x − 1 − x 泰勒 或洛必达 x → 0 lim 2 1 x 2 = 2 1 (2) 数一2021 设函数 f ( x , y ) f(x, y) f ( x , y ) f ( x + 1 , e x ) = x ( x + 1 ) 2 , f ( x , x 2 ) = 2 x 2 ln x f\left(x+1, \mathrm{e}^{x}\right)=x(x+1)^{2}, f\left(x, x^{2}\right)=2 x^{2} \ln x f ( x + 1 , e x ) = x ( x + 1 ) 2 , f ( x , x 2 ) = 2 x 2 ln x d f ( 1 , 1 ) = ( ) \mathrm{d} f(1,1)=(\quad) d f ( 1 , 1 ) = ( ) d x + d y \mathrm{d} x+\mathrm{d} y d x + d y d x − d y \mathrm{d} x-\mathrm{d} y d x − d y d y \mathrm{d} y d y − d y -\mathrm{d} y − d y
(2) 解 根据全微分的定义:d f ( 1 , 1 ) = f 1 ′ ( 1 , 1 ) d x + f 2 ′ ( 1 , 1 ) d y \mathrm{d} f(1,1)=f_1^{\prime}(1,1) \mathrm{d} x+f_2^{\prime}(1,1) \mathrm{d} y d f ( 1 , 1 ) = f 1 ′ ( 1 , 1 ) d x + f 2 ′ ( 1 , 1 ) d y 需要对 f ( x + 1 , e x ) = x ( x + 1 ) 2 f(x+1, \mathrm{e}^x) = x(x+1)^2 f ( x + 1 , e x ) = x ( x + 1 ) 2 f ( x , x 2 ) = 2 x 2 ln x f(x, x^2) = 2x^2 \ln x f ( x , x 2 ) = 2 x 2 ln x x x x 对 f ( x + 1 , e x ) = x ( x + 1 ) 2 → 等式左右都对 x 求导 f(x+1, \mathrm{e}^x) = x(x+1)^2\xrightarrow[]{\text{等式左右都对}x\text{求导}} f ( x + 1 , e x ) = x ( x + 1 ) 2 等式左右都对 x 求导 f 1 ′ ( x + 1 , e x ) + f 2 ′ ( x + 1 , e x ) ⋅ e x = ( x + 1 ) 2 + 2 x ( x + 1 ) \displaystyle f_1'(x+1, \mathrm{e}^x) + f_2'(x+1, \mathrm{e}^x) \cdot \mathrm{e}^x = (x+1)^2 + 2x(x+1) f 1 ′ ( x + 1 , e x ) + f 2 ′ ( x + 1 , e x ) ⋅ e x = ( x + 1 ) 2 + 2 x ( x + 1 ) 代入 x = 0 x=0 x = 0 f 1 ′ ( 1 , 1 ) + f 2 ′ ( 1 , 1 ) = 1 f_1'(1,1) + f_2'(1,1) = 1 f 1 ′ ( 1 , 1 ) + f 2 ′ ( 1 , 1 ) = 1 对 f ( x , x 2 ) = 2 x 2 ln x → 等式左右都对 x 求导 f(x, x^2) = 2x^2 \ln x\xrightarrow[]{\text{等式左右都对}x\text{求导}} f ( x , x 2 ) = 2 x 2 ln x 等式左右都对 x 求导 f 1 ′ ( x , x 2 ) + 2 x ⋅ f 2 ′ ( x , x 2 ) = 4 x ln x + 2 x \displaystyle f_1'(x, x^2) + 2x \cdot f_2'(x, x^2) = 4x \ln x + 2x f 1 ′ ( x , x 2 ) + 2 x ⋅ f 2 ′ ( x , x 2 ) = 4 x ln x + 2 x 代入 x = 1 x=1 x = 1 f 1 ′ ( 1 , 1 ) + 2 f 2 ′ ( 1 , 1 ) = 2 f_1'(1,1) + 2f_2'(1,1) = 2 f 1 ′ ( 1 , 1 ) + 2 f 2 ′ ( 1 , 1 ) = 2 联立方程组得到 f 1 ′ ( 1 , 1 ) = 0 f_1'(1,1) = 0 f 1 ′ ( 1 , 1 ) = 0 f 2 ′ ( 1 , 1 ) = 1 f_2'(1,1) = 1 f 2 ′ ( 1 , 1 ) = 1 写出全微分方程z = ∂ z ∂ u d u + ∂ z ∂ v d v z=\frac{\partial z}{\partial u} d u+\frac{\partial z}{\partial v} d v z = ∂ u ∂ z d u + ∂ v ∂ z d v d f ( 1 , 1 ) = f 1 ′ ( 1 , 1 ) d x + f 2 ′ ( 1 , 1 ) d y = 0 d x + 1 d y \mathrm{d}f(1,1) = f_1'(1,1)\mathrm{d}x + f_2'(1,1)\mathrm{d}y=0dx+1\mathrm{d}y d f ( 1 , 1 ) = f 1 ′ ( 1 , 1 ) d x + f 2 ′ ( 1 , 1 ) d y = 0 d x + 1 d y 高昆仑版 (3) 数一2021 设函数 f ( x ) = sin x 1 + x 2 f(x)=\frac{\sin x}{1+x^{2}} f ( x ) = 1 + x 2 s i n x x = 0 x=0 x = 0 a x + b x 2 + c x 3 a x+b x^{2}+c x^{3} a x + b x 2 + c x 3 a = 1 , b = 0 , c = − 7 6 a=1, b=0, c=-\frac{7}{6} a = 1 , b = 0 , c = − 6 7 a = 1 , b = 0 , c = 7 6 a=1, b=0, c=\frac{7}{6} a = 1 , b = 0 , c = 6 7 a = − 1 , b = − 1 , c = − 7 6 a=-1, b=-1, c=-\frac{7}{6} a = − 1 , b = − 1 , c = − 6 7 a = − 1 , b = − 1 , c = 7 6 a=-1, b=-1, c=\frac{7}{6} a = − 1 , b = − 1 , c = 6 7
(3) 数一2021 问题是求函数 f ( x ) = sin x 1 + x 2 f(x)=\frac{\sin x}{1+x^2} f ( x ) = 1 + x 2 s i n x x = 0 x=0 x = 0 a x + b x 2 + c x 3 a x + b x^2 + c x^3 a x + b x 2 + c x 3 f ( x ) = sin x ⋅ 1 1 + x 2 = ( x − 1 6 x 3 + … ) ⋅ ( 1 − x 2 + … ) \displaystyle f(x) = \sin x \cdot \frac{1}{1 + x^2} = \left( x - \frac{1}{6}x^3 + \ldots \right) \cdot \left( 1 - x^2 + \ldots \right) f ( x ) = sin x ⋅ 1 + x 2 1 = ( x − 6 1 x 3 + … ) ⋅ ( 1 − x 2 + … ) = x − x 3 − 1 6 x 3 + … \displaystyle = x - x^3 - \frac{1}{6}x^3 + \ldots = x − x 3 − 6 1 x 3 + … = x − 7 6 x 3 + … \displaystyle = x - \frac{7}{6}x^3 + \ldots = x − 6 7 x 3 + … 对比3次泰勒多项式: a x + b x 2 + c x 3 a x + b x^2 + c x^3 a x + b x 2 + c x 3 正确答案是 (B) a = 1 , b = 0 , c = − 7 6 a=1, b=0, c=-\frac{7}{6} a = 1 , b = 0 , c = − 6 7 sin x = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + ⋯ + ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! + ⋯ , − ∞ < x < + ∞ . \displaystyle \sin x=\sum_{n=0}^{\infty}(-1)^n \frac{x^{2 n+1}}{(2 n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots+(-1)^n \frac{x^{2 n+1}}{(2 n+1)!}+\cdots,-\infty<x<+\infty . sin x = n = 0 ∑ ∞ ( − 1 ) n ( 2 n + 1 )! x 2 n + 1 = x − 3 ! x 3 + 5 ! x 5 − 7 ! x 7 + ⋯ + ( − 1 ) n ( 2 n + 1 )! x 2 n + 1 + ⋯ , − ∞ < x < + ∞. 1 1 + x = ∑ n = 0 ∞ ( − 1 ) n x n = 1 − x + x 2 − x 3 + ⋯ + ( − 1 ) n x n + ⋯ , − 1 < x < 1. \displaystyle \frac{1}{1+x}=\sum_{n=0}^{\infty}(-1)^n x^n=1-x+x^2-x^3+\cdots+(-1)^n x^n+\cdots,-1<x<1 . 1 + x 1 = n = 0 ∑ ∞ ( − 1 ) n x n = 1 − x + x 2 − x 3 + ⋯ + ( − 1 ) n x n + ⋯ , − 1 < x < 1. (4) 数一2021 设函数 f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ] ∫ 0 1 f ( x ) d x = ( ) \displaystyle \int_{0}^{1} f(x) \mathrm{d} x=(\quad) ∫ 0 1 f ( x ) d x = ( ) lim n → ∞ ∑ k = 1 n f ( 2 k − 1 2 n ) 1 2 n \displaystyle \lim _{n \rightarrow \infty} \sum_{k=1}^{n} f\left(\frac{2 k-1}{2 n}\right) \frac{1}{2 n} n → ∞ lim k = 1 ∑ n f ( 2 n 2 k − 1 ) 2 n 1 lim n → ∞ ∑ k = 1 n f ( 2 k − 1 2 n ) 1 n \displaystyle \lim _{n \rightarrow \infty} \sum_{k=1}^{n} f\left(\frac{2 k-1}{2 n}\right) \frac{1}{n} n → ∞ lim k = 1 ∑ n f ( 2 n 2 k − 1 ) n 1 lim n → ∞ ∑ k = 1 2 n f ( k − 1 2 n ) 1 n \displaystyle \lim _{n \rightarrow \infty} \sum_{k=1}^{2 n} f\left(\frac{k-1}{2 n}\right) \frac{1}{n} n → ∞ lim k = 1 ∑ 2 n f ( 2 n k − 1 ) n 1 lim n → ∞ ∑ k = 1 2 n f ( k 2 n ) 2 n \displaystyle \lim _{n \rightarrow \infty} \sum_{k=1}^{2 n} f\left(\frac{k}{2 n}\right) \frac{2}{n} n → ∞ lim k = 1 ∑ 2 n f ( 2 n k ) n 2
(4) 只需要1 n 与 i n \frac{1}{n} \text{与}\frac{i}{n} n 1 与 n i 1 2 n 与 i 2 n \frac{1}{2n} \text{与} \frac{i}{2n} 2 n 1 与 2 n i 分析选项 (B) 将 [ 0 , 1 ] [0,1] [ 0 , 1 ] n n n 每个小区间为 [ k − 1 n , k n ] \left[\frac{k-1}{n}, \frac{k}{n}\right] [ n k − 1 , n k ] 区间长度为 1 n \frac{1}{n} n 1 在 [ k − 1 n , k n ] \left[\frac{k-1}{n}, \frac{k}{n}\right] [ n k − 1 , n k ] f ( k n + k − 1 n 2 ) f\left(\frac{\frac{k}{n}+\frac{k-1}{n}}{2}\right) f ( 2 n k + n k − 1 ) 2 k − 1 2 n \frac{2k-1}{2n} 2 n 2 k − 1 = lim n → ∞ ( 1 n ⋅ f ( 0 + 1 n 2 ) + 1 n ⋅ f ( 1 n + 2 n 2 ) + … + 1 n ⋅ f ( n − 1 n + 1 2 ) ) \displaystyle = \lim_{n \to \infty} \left( \frac{1}{n} \cdot f\left( \frac{0 + \frac{1}{n}}{2} \right) + \frac{1}{n} \cdot f\left( \frac{\frac{1}{n} + \frac{2}{n}}{2} \right) + \ldots + \frac{1}{n} \cdot f\left( \frac{\frac{n-1}{n} + 1}{2} \right) \right) = n → ∞ lim ( n 1 ⋅ f ( 2 0 + n 1 ) + n 1 ⋅ f ( 2 n 1 + n 2 ) + … + n 1 ⋅ f ( 2 n n − 1 + 1 ) ) = lim n → ∞ ( 1 n ⋅ f ( 1 2 n ) + 1 n ⋅ f ( 3 2 n ) + … + 1 n ⋅ f ( 2 n − 1 2 n ) ) \displaystyle = \lim_{n \to \infty} \left( \frac{1}{n} \cdot f\left( \frac{1}{2n} \right) + \frac{1}{n} \cdot f\left( \frac{3}{2n} \right) + \ldots + \frac{1}{n} \cdot f\left( \frac{2n-1}{2n} \right) \right) = n → ∞ lim ( n 1 ⋅ f ( 2 n 1 ) + n 1 ⋅ f ( 2 n 3 ) + … + n 1 ⋅ f ( 2 n 2 n − 1 ) ) 根据定积分定义 得 ∫ 0 1 f ( x ) d x = lim n → ∞ ∑ k = 1 n f ( 2 k − 1 2 n ) ⋅ 1 n \displaystyle \int_0^1 f(x) \mathrm{d} x = \lim_{n \rightarrow \infty} \sum_{k=1}^n f\left(\frac{2k-1}{2n}\right) \cdot \frac{1}{n} ∫ 0 1 f ( x ) d x = n → ∞ lim k = 1 ∑ n f ( 2 n 2 k − 1 ) ⋅ n 1 分析其他选项 (A), (C), (D) 选项 (A),得到 1 2 ∫ 0 1 f ( x ) d x \displaystyle \frac{1}{2} \int_0^1 f(x) \mathrm{d} x 2 1 ∫ 0 1 f ( x ) d x 选项 (C),得到 2 ∫ 0 1 f ( x ) d x \displaystyle 2 \int_0^1 f(x) \mathrm{d} x 2 ∫ 0 1 f ( x ) d x 选项 (D),得到 4 ∫ 0 1 f ( x ) d x \displaystyle 4 \int_0^1 f(x) \mathrm{d} x 4 ∫ 0 1 f ( x ) d x 结论:答案是 (B) (5) 数一2021 二次型 f ( x 1 , x 2 , x 3 ) = ( x 1 + x 2 ) 2 + ( x 2 + x 3 ) 2 − ( x 3 − x 1 ) 2 f\left(x_{1}, x_{2}, x_{3}\right)=\left(x_{1}+x_{2}\right)^{2}+\left(x_{2}+x_{3}\right)^{2}-\left(x_{3}-x_{1}\right)^{2} f ( x 1 , x 2 , x 3 ) = ( x 1 + x 2 ) 2 + ( x 2 + x 3 ) 2 − ( x 3 − x 1 ) 2 ( ) (\quad) ( )
(5) 这个问题是关于计算二次型的正惯性指数和负惯性指数的。解题步骤如下: 展开并化简二次型 f ( x 1 , x 2 , x 3 ) f(x_1, x_2, x_3) f ( x 1 , x 2 , x 3 ) 将 f ( x 1 , x 2 , x 3 ) f(x_1, x_2, x_3) f ( x 1 , x 2 , x 3 ) f ( x 1 , x 2 , x 3 ) = ( x 1 + x 2 ) 2 + ( x 2 + x 3 ) 2 − ( x 3 − x 1 ) 2 \displaystyle f\left(x_1, x_2, x_3\right)= \left(x_1+x_2\right)^2+\left(x_2+x_3\right)^2-\left(x_3-x_1\right)^2 f ( x 1 , x 2 , x 3 ) = ( x 1 + x 2 ) 2 + ( x 2 + x 3 ) 2 − ( x 3 − x 1 ) 2 = x 1 2 + 2 x 1 x 2 + x 2 2 + x 2 2 + 2 x 2 x 3 + x 3 2 − x 3 2 + 2 x 1 x 3 − x 1 2 =x_1^2+2 x_1 x_2+x_2^2+x_2^2+2 x_2 x_3+x_3^2-x_3^2+2 x_1 x_3-x_1^2 = x 1 2 + 2 x 1 x 2 + x 2 2 + x 2 2 + 2 x 2 x 3 + x 3 2 − x 3 2 + 2 x 1 x 3 − x 1 2 = 2 x 2 2 + 2 x 1 x 2 + 2 x 2 x 3 + 2 x 1 x 3 . =2 x_2^2+2 x_1 x_2+2 x_2 x_3+2 x_1 x_3 . = 2 x 2 2 + 2 x 1 x 2 + 2 x 2 x 3 + 2 x 1 x 3 . 得到 2 x 2 2 + 2 x 1 x 2 + 2 x 2 x 3 + 2 x 1 x 3 2x_2^2 + 2x_1x_2 + 2x_2x_3 + 2x_1x_3 2 x 2 2 + 2 x 1 x 2 + 2 x 2 x 3 + 2 x 1 x 3 写成矩阵 A = [ 0 1 1 1 2 1 1 1 0 ] \displaystyle A = \left[\begin{array}{ccc} 0 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 0\end{array}\right] A = 0 1 1 1 2 1 1 1 0 计算特征多项式 ∣ λ E − A ∣ |\lambda E - A| ∣ λ E − A ∣ ∣ λ E − A ∣ = ∣ λ − 1 − 1 − 1 λ − 2 − 1 − 1 − 1 λ ∣ = r 1 − r 3 两行相减为 0 并且形成公因式 ∣ λ + 10 − λ − 1 − 1 λ − 2 − 1 − 1 − 1 λ ∣ \displaystyle |\lambda \boldsymbol{E}-\boldsymbol{A}|=\left|\begin{array}{ccc}\lambda -1 -1 \\-1 \lambda-2 -1 \\-1 -1 \lambda\end{array}\right|\xlongequal[]{\begin {array}{l}r_1-r_{3}\text{两行相减为}0\\\text{并且形成公因式}\end{array}}\left|\begin{array}{ccc}\lambda+1 0 -\lambda-1 \\-1 \lambda-2 -1 \\-1 -1 \lambda\end{array}\right| ∣ λ E − A ∣ = λ − 1 − 1 − 1 λ − 2 − 1 − 1 − 1 λ r 1 − r 3 两行相减为 0 并且形成公因式 λ + 10 − λ − 1 − 1 λ − 2 − 1 − 1 − 1 λ = c 3 + c 1 ∣ λ + 100 − 1 λ − 2 − 2 − 1 − 1 λ − 1 \displaystyle \xlongequal[]{c_{3}+c_{1}}\mid \begin{array}{ccc}\lambda+1 0 0 \\-1 \lambda-2 -2 \\-1 -1 \lambda-1\end{array} c 3 + c 1 ∣ λ + 100 − 1 λ − 2 − 2 − 1 − 1 λ − 1 = 按照第一行展开 ( λ + 1 ) ∣ 100 − 1 λ − 2 − 2 − 1 − 1 λ − 1 ∣ \displaystyle \xlongequal[]{\text{按照第一行展开}}(\lambda+1)\left|\begin{array}{ccc}1 0 0 \\-1 \lambda-2 -2 \\-1 -1 \lambda-1\end{array}\right| 按照第一行展开 ( λ + 1 ) 100 − 1 λ − 2 − 2 − 1 − 1 λ − 1 = ( λ + 1 ) [ ( λ − 2 ) ( λ − 1 ) − 2 ] → 先展开 [ λ 2 − 3 λ + 2 − 2 ] \displaystyle \begin{array}{l} =(\lambda+1)[(\lambda-2)(\lambda-1)-2] \xrightarrow[]{\text{先展开}\left[\lambda^2-3 \lambda+2-2\right]}\end{array} = ( λ + 1 ) [( λ − 2 ) ( λ − 1 ) − 2 ] 先展开 [ λ 2 − 3 λ + 2 − 2 ] = 因式分解 λ ( λ + 1 ) ( λ − 3 ) \displaystyle \xlongequal[]{\text{因式分解}}\lambda(\lambda+1)(\lambda-3) 因式分解 λ ( λ + 1 ) ( λ − 3 ) 计算得到 λ ( λ + 1 ) ( λ − 3 ) \lambda(\lambda + 1)(\lambda - 3) λ ( λ + 1 ) ( λ − 3 ) 特征值为 0 , − 1 , 3 0, -1, 3 0 , − 1 , 3 正惯性指数 p = 1 p = 1 p = 1 负惯性指数 q = 1 q = 1 q = 1 (6) 已知 α 1 = ( 1 0 1 ) , α 2 = ( 1 2 1 ) , α 3 = ( 3 1 2 ) \displaystyle \boldsymbol{\alpha}_{1}=\left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right), \boldsymbol{\alpha}_{2}=\left(\begin{array}{l}1 \\ 2 \\ 1\end{array}\right), \boldsymbol{\alpha}_{3}=\left(\begin{array}{l}3 \\ 1 \\ 2\end{array}\right) α 1 = 1 0 1 , α 2 = 1 2 1 , α 3 = 3 1 2 β 1 = α 1 , β 2 = α 2 − k β 1 , β 3 = α 3 − l 1 β 1 − l 2 β 2 ⏟ 正好对应施密特正交化 \underbrace{\boldsymbol{\beta}_{1}=\boldsymbol{\alpha}_{1}, \boldsymbol{\beta}_{2}=\boldsymbol{\alpha}_{2}-k \boldsymbol{\beta}_{1}, \boldsymbol{\beta}_{3}=\boldsymbol{\alpha}_{3}-l_{1} \boldsymbol{\beta}_{1}-l_{2} \boldsymbol{\beta}_{2}}_{\text{正好对应施密特正交化}} 正好对应施密特正交化 β 1 = α 1 , β 2 = α 2 − k β 1 , β 3 = α 3 − l 1 β 1 − l 2 β 2 β 1 \boldsymbol{\beta}_{1} β 1 β 2 , β 3 \boldsymbol{\beta}_{2}, \boldsymbol{\beta}_{3} β 2 , β 3 l 1 , l 2 l_{1}, l_{2} l 1 , l 2 ( ) (\quad) ( ) 5 2 , 1 2 \frac{5}{2}, \frac{1}{2} 2 5 , 2 1 − 5 2 , 1 2 -\frac{5}{2}, \frac{1}{2} − 2 5 , 2 1 5 2 , − 1 2 \frac{5}{2},-\frac{1}{2} 2 5 , − 2 1 − 5 2 , − 1 2 -\frac{5}{2},-\frac{1}{2} − 2 5 , − 2 1
(6) β 3 = α 3 − ( β 1 , α 3 ) ( β 1 , β 1 ) ⏟ l 1 β 1 − ( β 2 , α 3 ) ( β 2 , β 2 ) ⏟ l 2 β 2 \boldsymbol{\beta}_3 = \boldsymbol{\alpha}_3 - \underbrace{\frac{(\boldsymbol{\beta}_1, \boldsymbol{\alpha}_3)}{(\boldsymbol{\beta}_1, \boldsymbol{\beta}_1)}}_{l_1}\boldsymbol{\beta}_1 - \underbrace{\frac{(\boldsymbol{\beta}_2, \boldsymbol{\alpha}_3)}{(\boldsymbol{\beta}_2, \boldsymbol{\beta}_2)}}_{l_2}\boldsymbol{\beta}_2 β 3 = α 3 − l 1 ( β 1 , β 1 ) ( β 1 , α 3 ) β 1 − l 2 ( β 2 , β 2 ) ( β 2 , α 3 ) β 2 进行施密特正交化:对 α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 令 β 1 = α 1 = ( 1 0 1 ) \displaystyle \boldsymbol{\beta}_1 = \boldsymbol{\alpha}_1=\left(\begin{array}{l}1\\ 0 \\ 1\end{array}\right) β 1 = α 1 = 1 0 1 计算 β 2 = α 2 − ( β 1 , α 2 ) ( β 1 , β 1 ) β 1 \boldsymbol{\beta}_2 = \boldsymbol{\alpha}_2 - \frac{(\boldsymbol{\beta}_1, \boldsymbol{\alpha}_2)}{(\boldsymbol{\beta}_1, \boldsymbol{\beta}_1)} \boldsymbol{\beta}_1 β 2 = α 2 − ( β 1 , β 1 ) ( β 1 , α 2 ) β 1 计算内积 ( β 1 , α 2 ) = β 1 T α 2 = ( 1 , 0 , 1 ) ( 1 2 1 ) = 2 \displaystyle (\boldsymbol{\beta}_1, \boldsymbol{\alpha}_2)=\boldsymbol{\beta}_1^{\mathrm{T}} \boldsymbol{\alpha}_2=(1,0,1)\left(\begin{array}{l}1 \\ 2 \\ 1\end{array}\right)=2 ( β 1 , α 2 ) = β 1 T α 2 = ( 1 , 0 , 1 ) 1 2 1 = 2 计算内积 ( β 1 , β 1 ) = β 1 T β 1 = ( 1 , 0 , 1 ) ( 1 0 1 ) = 2 \displaystyle (\boldsymbol{\beta}_1, \boldsymbol{\beta}_1) = \boldsymbol{\beta}_1^{\mathrm{T}} \boldsymbol{\beta}_1=(1,0,1)\left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right)=2 ( β 1 , β 1 ) = β 1 T β 1 = ( 1 , 0 , 1 ) 1 0 1 = 2 得到 β 2 = ( 1 2 1 ) − 2 2 ( 1 0 1 ) = ( 0 2 0 ) \displaystyle \boldsymbol{\beta}_2 =\left(\begin{array}{l}1 \\2 \\1\end{array}\right)-\frac{2}{2}\left(\begin{array}{l}1 \\0 \\1\end{array}\right)=\left(\begin{array}{l}0 \\2 \\0\end{array}\right) β 2 = 1 2 1 − 2 2 1 0 1 = 0 2 0 计算 β 3 = α 3 − ( β 1 , α 3 ) ( β 1 , β 1 ) β 1 − ( β 2 , α 3 ) ( β 2 , β 2 ) β 2 \boldsymbol{\beta}_3 = \boldsymbol{\alpha}_3 - \frac{(\boldsymbol{\beta}_1, \boldsymbol{\alpha}_3)}{(\boldsymbol{\beta}_1, \boldsymbol{\beta}_1)} \boldsymbol{\beta}_1 - \frac{(\boldsymbol{\beta}_2, \boldsymbol{\alpha}_3)}{(\boldsymbol{\beta}_2, \boldsymbol{\beta}_2)} \boldsymbol{\beta}_2 β 3 = α 3 − ( β 1 , β 1 ) ( β 1 , α 3 ) β 1 − ( β 2 , β 2 ) ( β 2 , α 3 ) β 2 计算内积( β 1 , α 3 ) = β 1 T α 3 = ( 1 , 0 , 1 ) ( 3 1 2 ) = 5 \displaystyle (\boldsymbol{\beta}_1, \boldsymbol{\alpha}_3) =\boldsymbol{\beta}_1^{\mathrm{T}} \boldsymbol{\alpha}_3=(1,0,1)\left(\begin{array}{l}3 \\1 \\2\end{array}\right)=5 ( β 1 , α 3 ) = β 1 T α 3 = ( 1 , 0 , 1 ) 3 1 2 = 5 计算内积 ( β 2 , α 3 ) = β 2 T α 3 = ( 0 , 2 , 0 ) ( 3 1 2 ) = 2 , \displaystyle \left(\boldsymbol{\beta}_2, \boldsymbol{\alpha}_3\right)=\boldsymbol{\beta}_2^{\mathrm{T}} \boldsymbol{\alpha}_3=(0,2,0)\left(\begin{array}{l}3 \\1 \\2\end{array}\right)=2 \text {, } ( β 2 , α 3 ) = β 2 T α 3 = ( 0 , 2 , 0 ) 3 1 2 = 2 , 计算内积 ( β 2 , β 2 ) = β 2 T β 2 = ( 0 , 2 , 0 ) ( 0 2 0 ) = 4 \displaystyle \left(\boldsymbol{\beta}_2, \boldsymbol{\beta}_2\right)=\boldsymbol{\beta}_2^{\mathrm{T}} \boldsymbol{\beta}_2=(0,2,0)\left(\begin{array}{l}0 \\ 2 \\ 0\end{array}\right)=4 ( β 2 , β 2 ) = β 2 T β 2 = ( 0 , 2 , 0 ) 0 2 0 = 4 得到 β 3 = α 3 − 5 2 β 1 − 1 2 β 2 \boldsymbol{\beta}_3 = \boldsymbol{\alpha}_3 - \frac{5}{2} \boldsymbol{\beta}_1 - \frac{1}{2} \boldsymbol{\beta}_2 β 3 = α 3 − 2 5 β 1 − 2 1 β 2 确定 l 1 l_1 l 1 l 2 l_2 l 2 由上述计算可知 l 1 = 5 2 l_1 = \frac{5}{2} l 1 = 2 5 l 2 = 1 2 l_2 = \frac{1}{2} l 2 = 2 1 (7) 设 A , B \boldsymbol{A}, \boldsymbol{B} A , B n n n r ( A O O A T A ) = 2 r ( A ) \displaystyle r\left(\begin{array}{cc}\boldsymbol{A} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\end{array}\right)=2 r(\boldsymbol{A}) r ( A O O A T A ) = 2 r ( A ) r ( A A B O A T ) = 2 r ( A ) \displaystyle r\left(\begin{array}{cc}\boldsymbol{A} & \boldsymbol{A} \boldsymbol{B} \\ \boldsymbol{O} & \boldsymbol{A}^{\mathrm{T}}\end{array}\right)=2 r(\boldsymbol{A}) r ( A O A B A T ) = 2 r ( A ) r ( A B A O A A T ) = 2 r ( A ) \displaystyle r\left(\begin{array}{cc}\boldsymbol{A} & \boldsymbol{B} \boldsymbol{A} \\ \boldsymbol{O} & \boldsymbol{A} \boldsymbol{A}^{\mathrm{T}}\end{array}\right)=2 r(\boldsymbol{A}) r ( A O B A A A T ) = 2 r ( A ) r ( A O B A A T ) = 2 r ( A ) \displaystyle r\left(\begin{array}{cc}\boldsymbol{A} & \boldsymbol{O} \\ \boldsymbol{B} \boldsymbol{A} & \boldsymbol{A}^{\mathrm{T}}\end{array}\right)=2 r(\boldsymbol{A}) r ( A B A O A T ) = 2 r ( A )
(7) 答 应选 C. 解 由矩阵的秩的性质知, r ( A ) = r ( A T ) = r ( A A T ) = r ( A T A ) r(\boldsymbol{A})=r\left(\boldsymbol{A}^{\mathrm{T}}\right)=r\left(\boldsymbol{A A ^ { \mathrm { T } }}\right)=r\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right) r ( A ) = r ( A T ) = r ( A A T ) = r ( A T A ) 故 r ( A O O A T A ) = r ( A ) + r ( A T A ) = 2 r ( A ) \displaystyle r\left(\begin{array}{cc}\boldsymbol{A} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\end{array}\right)=r(A)+r\left(A^T A\right)=2 r(A) r ( A O O A T A ) = r ( A ) + r ( A T A ) = 2 r ( A ) 对于(B),因为A B \displaystyle AB A B A \displaystyle A A r [ A A B O A T ] = r [ A O O A T ] = r ( A ) + r ( A T ) = 2 r ( A ) . \displaystyle r\left[\begin{array}{cc} A & AB \\ O & A^T \end{array}\right] = r\left[\begin{array}{cc} A & O \\ O & A^T \end{array}\right] = r(A) + r(A^T) = 2r(A). r [ A O A B A T ] = r [ A O O A T ] = r ( A ) + r ( A T ) = 2 r ( A ) . 对于(C),B A BA B A 行变换 ,无法用A A A 而r [ A B A O A A T ] \displaystyle r\left[\begin{array}{cc} A & BA \\ O & AA^T \end{array}\right] r [ A O B A A A T ] r [ A O O A A T ] . r\left[\begin{array}{cc} A & O \\ O & AA^T \end{array}\right]. r [ A O O A A T ] . 对于(D),因为 B A \displaystyle BA B A A \displaystyle A A r [ A O B A A T ] = r [ A O O A T ] = r ( A ) + r ( A T ) = 2 r ( A ) . \displaystyle r\left[\begin{array}{ll} A & O \\ BA & A^T \end{array}\right] = r\left[\begin{array}{ll} A & O \\ O & A^T \end{array}\right] = r(A) + r(A^T) = 2r(A). r [ A B A O A T ] = r [ A O O A T ] = r ( A ) + r ( A T ) = 2 r ( A ) . (8) 设 A , B A, B A , B 0 < P ( B ) < 1 0<P(B)<1 0 < P ( B ) < 1 ( ) (\quad) ( ) P ( A ∣ B ) = P ( A ) P(A \mid B)=P(A) P ( A ∣ B ) = P ( A ) P ( A ∣ B ˉ ) = P ( A ) P(A \mid \bar{B})=P(A) P ( A ∣ B ˉ ) = P ( A ) P ( A ∣ B ) > P ( A ) P(A \mid B)>P(A) P ( A ∣ B ) > P ( A ) P ( A ˉ ∣ B ˉ ) > P ( A ˉ ) P(\bar{A} \mid \bar{B})>P(\bar{A}) P ( A ˉ ∣ B ˉ ) > P ( A ˉ ) P ( A ∣ B ) > P ( A ∣ B ˉ ) P(A \mid B)>P(A \mid \bar{B}) P ( A ∣ B ) > P ( A ∣ B ˉ ) P ( A ∣ B ) > P ( A ) P(A \mid B)>P(A) P ( A ∣ B ) > P ( A ) P ( A ∣ A ∪ B ) > P ( A ˉ ∣ A ∪ B ) P(A \mid A \cup B)>P(\bar{A} \mid A \cup B) P ( A ∣ A ∪ B ) > P ( A ˉ ∣ A ∪ B ) P ( A ) > P ( B ) P(A)>P(B) P ( A ) > P ( B )
小崔版 思路: 左侧的式子恒等变形,右侧的式子也恒等变形 最终能变成同一个式子 A 左侧:P ( A B ) P ( B ) = P ( A ) → 移项 P ( A B ) = P ( A ) P ( B ) \displaystyle \frac{P(A B)}{P(B)}=P(A) \xrightarrow[]{\text{移项}} P(A B)=P(A) P(B) P ( B ) P ( A B ) = P ( A ) 移项 P ( A B ) = P ( A ) P ( B ) 右侧:P ( A B ˉ ) P ( B ˉ ) = P ( A ) → 移项 P ( A B ˉ ) = P ( A ) P ( B ˉ ) → P ( B ˉ ) = 1 − P ( B ) 取对立事件 \displaystyle \frac{P(A \bar{B})}{P(\bar{B})}=P(A) \xrightarrow[]{\text{移项}} P(A \bar{B})=P(A) P(\bar{B})\xrightarrow[P(\bar{B})=1-P(B)]{\text{取对立事件}} P ( B ˉ ) P ( A B ˉ ) = P ( A ) 移项 P ( A B ˉ ) = P ( A ) P ( B ˉ ) 取对立事件 P ( B ˉ ) = 1 − P ( B ) P ( A ) − P ( A B ) = P ( A ) ( 1 − P ( B ) ) = P ( A ) − P ( A ) P ( B ) \displaystyle P(A)-P(A B)=P(A)(1-P(B) )=P(A)-P(A)P(B) P ( A ) − P ( A B ) = P ( A ) ( 1 − P ( B )) = P ( A ) − P ( A ) P ( B ) ⇔ P ( A B ) = P ( A ) P ( B ) \displaystyle \Leftrightarrow P(A B)=P(A) P(B) ⇔ P ( A B ) = P ( A ) P ( B ) B 左侧:若 P ( A ∣ B ) > P ( A ) \displaystyle P(A \mid B) > P(A) P ( A ∣ B ) > P ( A ) → P ( A B ) P ( B ) > P ( A ) 条件概率 P ( A B ) > P ( A ) P ( B ) \displaystyle \xrightarrow[\frac{P(AB)}{P(B)} > P(A)]{\text{条件概率}}P(AB) > P(A)P(B) 条件概率 P ( B ) P ( A B ) > P ( A ) P ( A B ) > P ( A ) P ( B ) 右侧:P ( A ˉ ∩ B ˉ ) P ( B ˉ ) > 1 − P ( A ) ⇔ 1 − P ( A + B ) 1 − P ( B ) > 1 − P ( A ) \displaystyle \frac{P(\bar{A} \cap \bar{B})}{P(\bar{B})} >1-P(A) \Leftrightarrow \frac{1-P(A+B)}{1-P(B)}>1-P(A) P ( B ˉ ) P ( A ˉ ∩ B ˉ ) > 1 − P ( A ) ⇔ 1 − P ( B ) 1 − P ( A + B ) > 1 − P ( A ) 1 − P ( A ) − P ( B ) + P ( A B ) 1 − P ( B ) > 1 − P ( A ) \displaystyle \frac{1-P(A)-P(B)+P(A B)}{1-P(B)}>1-P(A) 1 − P ( B ) 1 − P ( A ) − P ( B ) + P ( A B ) > 1 − P ( A ) 1 − P ( A ) − P ( B ) ‾ + P ( A B ) > 1 − P ( A ) − P ( B ) ‾ + P ( A ) P ( B ) \displaystyle \underline{1-P(A)-P(B)}+P(A B)>\underline{1-P(A)-P(B)} +P(A)P(B) 1 − P ( A ) − P ( B ) + P ( A B ) > 1 − P ( A ) − P ( B ) + P ( A ) P ( B ) C 左侧:P ( A B ) P ( B ) > P ( A ) − P ( A B ) 1 − P ( B ) \displaystyle \frac{P(A B)}{P(B)}>\frac{P(A)-P(A B)}{1-P(B)} P ( B ) P ( A B ) > 1 − P ( B ) P ( A ) − P ( A B ) → 交叉相乘 P ( A B ) − P ( B ) P ( A B ) > P ( A ) P ( B ) − P ( B ) P ( A B ) \displaystyle \xrightarrow[]{\text{交叉相乘}}P(A B)-P(B) P(A B)>P(A) P(B)-P(B) P(A B) 交叉相乘 P ( A B ) − P ( B ) P ( A B ) > P ( A ) P ( B ) − P ( B ) P ( A B ) 右侧:同B选项左侧 D不成立 (9) 设 ( X 1 , Y 1 ) , ( X 2 , Y 2 ) , ⋯ , ( X n , Y n ) \left(X_{1}, Y_{1}\right),\left(X_{2}, Y_{2}\right), \cdots,\left(X_{n}, Y_{n}\right) ( X 1 , Y 1 ) , ( X 2 , Y 2 ) , ⋯ , ( X n , Y n ) N ( μ 1 , μ 2 ; σ 1 2 , σ 2 2 ; ρ ) \displaystyle N\left(\mu_{1}, \mu_{2} ; \sigma_{1}^{2}, \sigma_{2}^{2} ; \rho\right) N ( μ 1 , μ 2 ; σ 1 2 , σ 2 2 ; ρ ) θ = μ 1 − μ 2 , X ˉ = 1 n ∑ i = 1 n X i , Y ˉ = 1 n ∑ i = 1 n Y i , θ ^ = X ˉ − Y ˉ \displaystyle \theta=\mu_{1}-\mu_{2}, \bar{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i}, \bar{Y}=\frac{1}{n} \sum_{i=1}^{n} Y_{i}, \hat{\theta}=\bar{X}-\bar{Y} θ = μ 1 − μ 2 , X ˉ = n 1 i = 1 ∑ n X i , Y ˉ = n 1 i = 1 ∑ n Y i , θ ^ = X ˉ − Y ˉ ( ) (\quad) ( ) θ ^ \hat{\theta} θ ^ θ \theta θ D ( θ ^ ) = σ 1 2 + σ 2 2 n \displaystyle D(\hat{\theta})=\frac{\sigma_{1}^{2}+\sigma_{2}^{2}}{n} D ( θ ^ ) = n σ 1 2 + σ 2 2 θ ^ \hat{\theta} θ ^ θ \theta θ D ( θ ^ ) = σ 1 2 + σ 2 2 n \displaystyle D(\hat{\theta})=\frac{\sigma_{1}^{2}+\sigma_{2}^{2}}{n} D ( θ ^ ) = n σ 1 2 + σ 2 2 θ ^ \hat{\theta} θ ^ θ \theta θ D ( θ ^ ) = σ 1 2 + σ 2 2 − 2 ρ σ 1 σ 2 n \displaystyle D(\hat{\theta})=\frac{\sigma_{1}^{2}+\sigma_{2}^{2}-2 \rho \sigma_{1} \sigma_{2}}{n} D ( θ ^ ) = n σ 1 2 + σ 2 2 − 2 ρ σ 1 σ 2 θ ^ \hat{\theta} θ ^ θ \theta θ D ( θ ^ ) = σ 1 2 + σ 2 2 − 2 ρ σ 1 σ 2 n \displaystyle D(\hat{\theta})=\frac{\sigma_{1}^{2}+\sigma_{2}^{2}-2 \rho \sigma_{1} \sigma_{2}}{n} D ( θ ^ ) = n σ 1 2 + σ 2 2 − 2 ρ σ 1 σ 2
(9) ρ = Cov ( X , Y ) D ( X ) D ( Y ) = E ( X Y ) − E ( X ) E ( Y ) D ( X ) D ( Y ) . \rho=\frac{\operatorname{Cov}(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}=\frac{E(X Y)-E(X) E(Y)}{\sqrt{D(X)} \sqrt{D(Y)}} . ρ = D ( X ) D ( Y ) Cov ( X , Y ) = D ( X ) D ( Y ) E ( X Y ) − E ( X ) E ( Y ) . 求样本期望 \displaystyle E ( θ ^ ) = E ( X ˉ − Y ˉ ) = E X ˉ − E Y ˉ ∠ E X − E Y = μ 1 − μ 2 = θ . E(\hat{\theta}) = E(\bar{X}-\bar{Y}) = E\bar{X} - E\bar{Y} \angle EX - EY = \mu_{1} - \mu_{2} = \theta. E ( θ ^ ) = E ( X ˉ − Y ˉ ) = E X ˉ − E Y ˉ ∠ EX − E Y = μ 1 − μ 2 = θ . 求样本方差 D ( θ ^ ) = θ = μ 1 − μ 2 D ( X ˉ − Y ˉ ) = 性质 D X ˉ + D Y ˉ − 2 Cov ( X ˉ , Y ˉ ) \displaystyle D(\hat{\theta}) \xlongequal[]{\theta=\mu_{1}-\mu_{2}} D(\bar{X}-\bar{Y}) \xlongequal[]{\text{性质}} D\bar{X} + D\bar{Y} - 2\operatorname{Cov}(\bar{X},\bar{Y}) D ( θ ^ ) θ = μ 1 − μ 2 D ( X ˉ − Y ˉ ) 性质 D X ˉ + D Y ˉ − 2 Cov ( X ˉ , Y ˉ ) Cov ( X ˉ , Y ˉ ) = ρ σ 1 σ 2 n \displaystyle \operatorname{Cov}(\bar{X}, \bar{Y}) = \frac{\rho \sigma_1 \sigma_2}{n} Cov ( X ˉ , Y ˉ ) = n ρ σ 1 σ 2 = D ( X ˉ ) = σ 1 2 n , D ( Y ˉ ) = σ 2 2 n ( 1 n D X + 1 n D Y − 2 Cov ( 1 n ∑ i = 1 n X i , 1 n ∑ i = 1 n Y i ) \displaystyle \xlongequal[]{D(\bar{X}) = \frac{\sigma_1^2}{n}\text{,}D(\bar{Y}) = \frac{\sigma_2^2}{n}}\left(\frac{1}{n} DX + \frac{1}{n} DY - 2 \operatorname{Cov}\left(\frac{1}{n}\sum_{i=1}^{n} X_{i}, \frac{1}{n}\sum_{i=1}^{n} Y_{i}\right)\right. D ( X ˉ ) = n σ 1 2 , D ( Y ˉ ) = n σ 2 2 ( n 1 D X + n 1 D Y − 2 Cov ( n 1 i = 1 ∑ n X i , n 1 i = 1 ∑ n Y i ) = 1 n σ 1 2 + 1 n σ 2 2 − 2 ⋅ 1 n ⋅ 1 n Cov ( ∑ i = 1 n X i , ∑ i = 1 n Y i ) \displaystyle = \frac{1}{n}\sigma_{1}^{2} + \frac{1}{n}\sigma_{2}^{2} - 2 \cdot \frac{1}{n} \cdot \frac{1}{n} \operatorname{Cov}\left(\sum_{i=1}^{n} X_{i}, \sum_{i=1}^{n} Y_{i}\right) = n 1 σ 1 2 + n 1 σ 2 2 − 2 ⋅ n 1 ⋅ n 1 Cov ( i = 1 ∑ n X i , i = 1 ∑ n Y i ) { X 1 , Y 1 ⋯ … X 1 , Y n , ⋯ , { X n , Y 1 ⋯ … X n , Y n \displaystyle \left\{\begin{array}{l}X_1, Y_1 \\ \cdots \ldots \\ X_1, Y_n\end{array}, \cdots,\left\{\begin{array}{l}X_n, Y_1 \\ \cdots \ldots \\ X_n, Y_n\end{array}\right.\right. ⎩ ⎨ ⎧ X 1 , Y 1 ⋯… X 1 , Y n , ⋯ , ⎩ ⎨ ⎧ X n , Y 1 ⋯… X n , Y n = 处理协方差 1 n σ 1 2 + 1 n σ 2 2 − 2 ⋅ 1 n ⋅ 1 n ⋅ n Cov ( X 1 , Y 1 ) \displaystyle \xlongequal[]{\text{处理协方差}}\frac{1}{n}\sigma_{1}^{2} + \frac{1}{n}\sigma_{2}^{2} - 2 \cdot \frac{1}{n} \cdot \frac{1}{n} \cdot n \operatorname{Cov}(X_{1}, Y_{1}) 处理协方差 n 1 σ 1 2 + n 1 σ 2 2 − 2 ⋅ n 1 ⋅ n 1 ⋅ n Cov ( X 1 , Y 1 ) = ρ = Cov ( X , Y ) D ( X ) D ( Y ) 1 n σ 1 2 + 1 n σ 2 2 − 2 n ⋅ ρ ⋅ σ 1 ⋅ σ 2 . \displaystyle \xlongequal[]{\rho=\frac{\operatorname{Cov}(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}}\frac{1}{n}\sigma_{1}^{2} + \frac{1}{n}\sigma_{2}^{2} - \frac{2}{n} \cdot \rho \cdot \sigma_{1} \cdot \sigma_{2}. ρ = D ( X ) D ( Y ) Cov ( X , Y ) n 1 σ 1 2 + n 1 σ 2 2 − n 2 ⋅ ρ ⋅ σ 1 ⋅ σ 2 . 综上,θ ^ \hat{\theta} θ ^ θ \theta θ σ 1 2 + σ 2 2 − 2 ρ σ 1 σ 2 n \displaystyle \frac{\sigma_1^2 + \sigma_2^2 - 2 \rho \sigma_1 \sigma_2}{n} n σ 1 2 + σ 2 2 − 2 ρ σ 1 σ 2 (10) 设 X 1 , X 2 , ⋯ , X 16 X_{1}, X_{2}, \cdots, X_{16} X 1 , X 2 , ⋯ , X 16 N ( μ , 4 ) N(\mu, 4) N ( μ , 4 ) H 0 : μ ⩽ 10 H_{0}: \mu \leqslant 10 H 0 : μ ⩽ 10 H 1 : μ > 10 , Φ ( x ) H_{1}: \mu>10, \Phi(x) H 1 : μ > 10 , Φ ( x ) W = { X ˉ > 11 } W=\{\bar{X}>11\} W = { X ˉ > 11 } X ˉ = 1 16 ∑ i = 1 16 X i \displaystyle \bar{X}=\frac{1}{16} \sum_{i=1}^{16} X_{i} X ˉ = 16 1 i = 1 ∑ 16 X i μ = 11.5 \mu=11.5 μ = 11.5 ( ) (\quad) ( ) 1 − Φ ( 0.5 ) 1-\Phi(0.5) 1 − Φ ( 0.5 ) 1 − Φ ( 1 ) 1-\Phi(1) 1 − Φ ( 1 ) 1 − Φ ( 1.5 ) 1-\Phi(1.5) 1 − Φ ( 1.5 ) 1 − Φ ( 2 ) 1-\Phi(2) 1 − Φ ( 2 )
(10) [01:07:54](file:///C:/Users/wangpanfeng/Videos/01.%E6%95%B0%E5%AD%A6%E4%B8%80/08.2021%E5%B9%B4%E6%95%B0%E4%B8%80%E7%9C%9F%E9%A2%98/01.2021%E5%B9%B4%E8%80%83%E7%A0%94%E6%95%B0%E5%AD%A6%E7%9C%9F%E9%A2%98%E9%80%89%E6%8B%A9%E9%A2%98%EF%BC%88%E6%95%B0%E4%B8%80%EF%BC%89.mp4#t=1:07:54) (1)两类错误 (1)第一类错误 (弃真错误): 当原假设 H 0 H_0 H 0 H 0 H_0 H 0 (2)第二类错误 (存伪错误): 当原假设 H 0 H_0 H 0 H 0 H_0 H 0 根据已知条件, μ = 11.5 \mu=11.5 μ = 11.5 H 0 : μ ⩽ 10 H_0: \mu \leqslant 10 H 0 : μ ⩽ 10 由于该检验问题的拒绝域为 W = { X ˉ > 11 } W=\{\bar{X}>11\} W = { X ˉ > 11 } 得到接受域:X ˉ ⩽ 11 \bar{X} \leqslant 11 X ˉ ⩽ 11 故当 X ˉ ⩽ 11 \bar{X} \leqslant 11 X ˉ ⩽ 11 H 0 H_0 H 0 P { X ˉ ⩽ 11 } P\{\bar{X} \leqslant 11\} P { X ˉ ⩽ 11 } 下面我们计算 P { X ˉ ⩽ 11 } P\{\bar{X} \leqslant 11\} P { X ˉ ⩽ 11 } 由样本均值 X ˉ = 1 16 ∑ i = 1 16 X i \displaystyle \bar{X} = \frac{1}{16} \sum_{i=1}^{16} X_i X ˉ = 16 1 i = 1 ∑ 16 X i n = 16 n = 16 n = 16 故 X ˉ ∼ N ( μ , 4 16 ) \bar{X} \sim N\left(\mu, \frac{4}{16}\right) X ˉ ∼ N ( μ , 16 4 ) → μ = 11.5 X ˉ ∼ N ( 11.5 , 1 4 ) \xrightarrow[]{\mu=11.5}\bar{X} \sim N\left(11.5, \frac{1}{4}\right) μ = 11.5 X ˉ ∼ N ( 11.5 , 4 1 ) X ˉ − 11.5 1 2 ∼ N ( 0 , 1 ) \frac{\bar{X}-11.5}{\frac{1}{2}} \sim N(0,1) 2 1 X ˉ − 11.5 ∼ N ( 0 , 1 ) P { X ˉ ⩽ 11 } = P { X ˉ − 11.5 1 2 ⩽ 11 − 11.5 1 2 } = Φ ( − 1 ) = 1 − Φ ( 1 ) P\{\bar{X} \leqslant 11\}=P\left\{\frac{\bar{X}-11.5}{\frac{1}{2}} \leqslant \frac{11-11.5}{\frac{1}{2}}\right\}=\Phi(-1)=1-\Phi(1) P { X ˉ ⩽ 11 } = P { 2 1 X ˉ − 11.5 ⩽ 2 1 11 − 11.5 } = Φ ( − 1 ) = 1 − Φ ( 1 ) 选项中没有Φ ( − 1 ) \Phi(-1) Φ ( − 1 ) Φ ( 1 ) \Phi(1) Φ ( 1 ) 犯第二类错误落在接受域的概率:1 − Φ ( 1 ) 1 - \Phi(1) 1 − Φ ( 1 ) (2018)设总体 X X X N ( μ , σ 2 ) . X 1 , X 2 , ⋯ , X n \displaystyle N\left(\mu, \sigma^{2}\right) . X_{1}, X_{2}, \cdots, X_{n} N ( μ , σ 2 ) . X 1 , X 2 , ⋯ , X n X X X H 0 : μ = μ 0 , H 1 : μ ≠ μ 0 H_{0}: \mu=\mu_{0}, H_{1}: \mu \neq \mu_{0} H 0 : μ = μ 0 , H 1 : μ = μ 0 (A) 如果在检验水平 α = 0.05 \alpha=0.05 α = 0.05 H 0 H_{0} H 0 α = 0.01 \alpha=0.01 α = 0.01 H 0 H_{0} H 0 (B) 如果在检验水平 α = 0.05 \alpha=0.05 α = 0.05 H 0 H_{0} H 0 α = 0.01 \alpha=0.01 α = 0.01 H 0 H_{0} H 0 (C) 如果在检验水平 α = 0.05 \alpha=0.05 α = 0.05 H 0 H_{0} H 0 α = 0.01 \alpha=0.01 α = 0.01 H 0 H_{0} H 0 (D) 如果在检验水平 α = 0.05 \alpha=0.05 α = 0.05 H 0 H_{0} H 0 α = 0.01 \alpha=0.01 α = 0.01 H 0 H_{0} H 0 二、填空题 (本题共 6 小题,每小题 5 分,共 30 分, 把答案填在题中横线.上.)}
(11) ∫ 0 + ∞ 1 x 2 + 2 x + 2 d x = \displaystyle \int_{0}^{+\infty} \frac{1}{x^{2}+2 x+2} \mathrm{~d} x= ∫ 0 + ∞ x 2 + 2 x + 2 1 d x =
(11) 答 应填 π 4 \frac{\pi}{4} 4 π
高昆仑版 ∫ 0 + ∞ 1 x 2 + 2 x + 2 d x = ∫ 0 + ∞ 1 ( x + 1 ) 2 + 1 d x \displaystyle \int_{0}^{+\infty} \frac{1}{x^{2}+2x+2} \, dx = \int_{0}^{+\infty} \frac{1}{(x+1)^{2}+1} \, dx ∫ 0 + ∞ x 2 + 2 x + 2 1 d x = ∫ 0 + ∞ ( x + 1 ) 2 + 1 1 d x = ∫ 1 1 + u 2 d u = arctan ( u ) arctan ( x + 1 ) ∣ 0 + ∞ \displaystyle \xlongequal[]{\int \frac1{1+u^2}du=\arctan(u)} \left. \arctan(x+1) \right|_{0}^{+\infty} ∫ 1 + u 2 1 d u = a r c t a n ( u ) arctan ( x + 1 ) ∣ 0 + ∞ = arctan ( 1 ) = π 4 arctan ( + ∞ ) = π 2 π 2 − π 4 = π 4 . \displaystyle \xlongequal[\arctan(1) = \frac{\pi}{4}]{\arctan(+\infty) = \frac{\pi}{2}}\frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}. a r c t a n ( + ∞ ) = 2 π a r c t a n ( 1 ) = 4 π 2 π − 4 π = 4 π . gpt版 计算积分 ∫ 0 + ∞ 1 x 2 + 2 x + 2 d x \displaystyle \int_{0}^{+\infty} \frac{1}{x^2 + 2x + 2} \, dx ∫ 0 + ∞ x 2 + 2 x + 2 1 d x 式子化简 分母化简:x 2 + 2 x + 2 x^2 + 2x + 2 x 2 + 2 x + 2 x 2 + 2 x + 1 + 1 x^2 + 2x + 1 + 1 x 2 + 2 x + 1 + 1 完全平方:( x + 1 ) 2 + 1 (x + 1)^2 + 1 ( x + 1 ) 2 + 1 新积分形式:∫ 0 + ∞ 1 ( x + 1 ) 2 + 1 d ( x + 1 ) \displaystyle \int_0^{+\infty} \frac{1}{(x + 1)^2 + 1} \, d(x+1) ∫ 0 + ∞ ( x + 1 ) 2 + 1 1 d ( x + 1 ) 计算积分 使用反正切函数:∫ 1 1 + u 2 d u = arctan ( u ) \displaystyle \int \frac1{1+u^2}du=\arctan(u) ∫ 1 + u 2 1 d u = arctan ( u ) 积分结果:= arctan ( x + 1 ) ∣ 0 + ∞ = arctan ( 1 ) = π 4 arctan ( + ∞ ) = π 2 π 2 − π 4 = π 4 =\left. \arctan(x + 1) \right|_0^{+\infty}\xlongequal[\arctan(1) = \frac{\pi}{4}]{\arctan(+\infty) = \frac{\pi}{2}}\frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4} = arctan ( x + 1 ) ∣ 0 + ∞ a r c t a n ( + ∞ ) = 2 π a r c t a n ( 1 ) = 4 π 2 π − 4 π = 4 π (12) 设函数 y = y ( x ) y=y(x) y = y ( x ) { x = 2 e t + t + 1 , y = 4 ( t − 1 ) e t + t 2 \displaystyle \left\{\begin{array}{l}x=2 \mathrm{e}^{t}+t+1, \\ y=4(t-1) \mathrm{e}^{t}+t^{2}\end{array}\right. { x = 2 e t + t + 1 , y = 4 ( t − 1 ) e t + t 2 d 2 y d x 2 ∣ t = 0 = \left.\frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}\right|_{t=0}= d x 2 d 2 y t = 0 = d y d x = y ′ ( t ) x ′ ( t ) = 4 e t + 4 ( t − 1 ) e t + 2 t 2 e t + 1 ≈ 2 t , \displaystyle \frac{dy}{dx} = \frac{y'(t)}{x'(t)} = \frac{4e^t + 4(t-1)e^t + 2t}{2e^t + 1} \approx 2t, d x d y = x ′ ( t ) y ′ ( t ) = 2 e t + 1 4 e t + 4 ( t − 1 ) e t + 2 t ≈ 2 t , d 2 y d x 2 ∣ t = 0 = d ( 2 t ) d t ⋅ 1 x ′ ( t ) ∣ t = 0 = 2 2 e t + 1 ∣ t = 0 = 2 3 . \displaystyle \left. \frac{d^2y}{dx^2} \right|_{t=0} = \left. \frac{d(2t)}{dt} \cdot \frac{1}{x'(t)} \right|_{t=0} = \left. \frac{2}{2e^t + 1} \right|_{t=0} = \frac{2}{3}. d x 2 d 2 y t = 0 = d t d ( 2 t ) ⋅ x ′ ( t ) 1 t = 0 = 2 e t + 1 2 t = 0 = 3 2 . (13) 欧拉方程 x 2 y ′ ′ + x y ′ − 4 y = 0 x^{2} y^{\prime \prime}+x y^{\prime}-4 y=0 x 2 y ′′ + x y ′ − 4 y = 0 y ( 1 ) = 1 , y ′ ( 1 ) = 2 y(1)=1, y^{\prime}(1)=2 y ( 1 ) = 1 , y ′ ( 1 ) = 2 y = y= y =
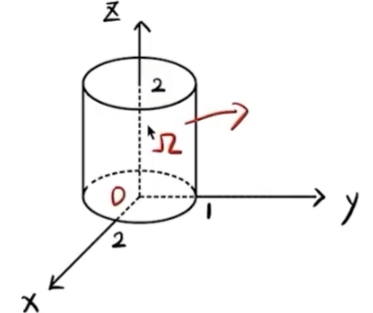
(13) x = e t , x 2 y ′ ′ = D ( D − 1 ) y , x y ′ = D y , D = d d t \displaystyle x = e^t, \quad x^2 y'' = D(D-1) y, \quad x y' = D y, \quad D = \frac{d}{dt} x = e t , x 2 y ′′ = D ( D − 1 ) y , x y ′ = Dy , D = d t d D ( D − 1 ) y + D y − 4 y = 0 \displaystyle D(D-1) y + D y - 4y = 0 D ( D − 1 ) y + Dy − 4 y = 0 → 整理 D 2 y − 4 y = 0 \displaystyle \xrightarrow[]{\text{整理}} D^2 y - 4y = 0 整理 D 2 y − 4 y = 0 → D = d d t d 2 y d t 2 − 4 y = 0 \displaystyle \xrightarrow[]{D = \frac{d}{dt} }\frac{d^2 y}{dt^2} - 4y = 0 D = d t d d t 2 d 2 y − 4 y = 0 → 求特征方程 λ 2 − 4 = 0 \displaystyle \xrightarrow[]{\text{求特征方程}}\lambda^2 - 4 = 0 求特征方程 λ 2 − 4 = 0 λ = ± 2 \displaystyle \lambda = \pm 2 λ = ± 2 → 通解公式 y = C 1 e 2 t + C 2 e − 2 t \displaystyle \xrightarrow[]{\text{通解公式}} y = C_1 e^{2t} + C_2 e^{-2t} 通解公式 y = C 1 e 2 t + C 2 e − 2 t { y = C 1 x 2 + C 2 x − 2 ← y ( 1 ) = 1 y ′ = 2 C 1 x − 2 C 2 x − 3 ← y ′ ( 1 ) = 2 \displaystyle \begin{cases} y = C_1 x^2 + C_2 x^{-2} \leftarrow y(1) = 1 \\y' = 2C_1 x - 2C_2 x^{-3} \leftarrow y'(1) = 2\end{cases} { y = C 1 x 2 + C 2 x − 2 ← y ( 1 ) = 1 y ′ = 2 C 1 x − 2 C 2 x − 3 ← y ′ ( 1 ) = 2 { 1 = C 1 + C 2 1 = C 1 − C 2 \displaystyle \begin{cases}1 = C_1 + C_2 \\1 = C_1 - C_2 \\\end{cases} { 1 = C 1 + C 2 1 = C 1 − C 2 C 1 = 1 \displaystyle C_1=1 C 1 = 1 C 2 = 0 C_2=0 C 2 = 0 → 代入原式 y = x 2 \xrightarrow[]{\text{代入原式}}y = x^2 代入原式 y = x 2 2004 年数一试题欧拉方程x 2 d 2 y d x 2 + 4 x d y d x + 2 y = 0 ( x > 0 ) x^2 \frac{\mathrm{~d}^2 y}{\mathrm{~d} x^2}+4 x \frac{\mathrm{~d} y}{\mathrm{~d} x}+2 y=0(x>0) x 2 d x 2 d 2 y + 4 x d x d y + 2 y = 0 ( x > 0 ) \qquad (14) 设 Σ \displaystyle \Sigma Σ { ( x , y , z ) ∣ x 2 + 4 y 2 ⩽ 4 , 0 ⩽ z ⩽ 2 } \left\{(x, y, z) \mid x^{2}+4 y^{2} \leqslant 4,0 \leqslant z \leqslant 2\right\} { ( x , y , z ) ∣ x 2 + 4 y 2 ⩽ 4 , 0 ⩽ z ⩽ 2 } ∬ Σ x 2 d y d z + \displaystyle \iint_{\Sigma} x^{2} \mathrm{~d} y \mathrm{~d} z+ ∬ Σ x 2 d y d z + y 2 d z d x + z d x d y = y^{2} \mathrm{~d} z \mathrm{~d} x+z \mathrm{~d} x \mathrm{~d} y= y 2 d z d x + z d x d y =
(14) 解 利用高斯公式,得 \displaystyle = ∮ Σ x 2 d y d z + y 2 d z d x + z d x d y = \oint_\Sigma x^2 \, dy \, dz + y^2 \, dz \, dx + z \, dx \, dy = ∮ Σ x 2 d y d z + y 2 d z d x + z d x d y = 高斯 ∭ Ω ( 2 x + 2 y + 1 ) d v \displaystyle \xlongequal[]{\text{高斯}} \iiint_\Omega (2x + 2y + 1) \, dv 高斯 ∭ Ω ( 2 x + 2 y + 1 ) d v = x , y 奇函数为 0 0 + ∭ Ω 1 d v = V Ω = π a b × h 求圆柱体体积 π ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 4 4 π . \displaystyle \xlongequal[x\text{,}y]{\text{奇函数为}0}0 + \iiint_\Omega 1 \, dv = V_\Omega \xlongequal[\pi ab\times h]{\text{求圆柱体体积}} \pi \cdot 2 \cdot 1 \cdot 2 \cdot \frac{4}{4} \pi. 奇函数为 0 x , y 0 + ∭ Ω 1 d v = V Ω 求圆柱体体积 πab × h π ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 4 4 π . (15) 设 A = ( a i j ) \boldsymbol{A}=\left(a_{i j}\right) A = ( a ij ) A i j A_{i j} A ij a i j a_{i j} a ij A \boldsymbol{A} A ∣ A ∣ = |\boldsymbol{A}|= ∣ A ∣ = A 11 + A 21 + A 31 = A_{11}+A_{21}+A_{31}= A 11 + A 21 + A 31 =
(15) 答案 方法2:构造一个行列式 由每行元素之和等于2\to往这里恒等变形,和构造新的行列式 ( 2 ) ∣ A ∣ = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = c 1 + c 2 + c 3 ∣ a 11 + a 12 + a 13 a 12 a 13 a 21 + a 22 + a 23 a 22 a 23 a 31 + a 32 + a 33 a 32 a 33 ∣ \displaystyle (2)|A|=\left|\begin{array}{lll}a_{11} a_{12} a_{13} \\ a_{21} a_{22} a_{23} \\ a_{31} a_{32} a_{33}\end{array}\right|\xlongequal[]{c_1+c_2+c_3}\left|\begin{array}{lll}a_{11}+a_{12}+a_{13} a_{12} a_{13} \\ a_{21}+a_{22}+a_{23} a_{22} a_{23} \\ a_{31}+a_{32}+a_{33} a_{32} a_{33}\end{array}\right| ( 2 ) ∣ A ∣ = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 c 1 + c 2 + c 3 a 11 + a 12 + a 13 a 12 a 13 a 21 + a 22 + a 23 a 22 a 23 a 31 + a 32 + a 33 a 32 a 33 将每行元素之和等于2代入,得= ∣ 2 a 12 a 13 2 a 22 a 23 2 a 32 a 33 ∣ \displaystyle =\left|\begin{array}{lll}2 & a_{12} & a_{13} \\ 2 & a_{22} & a_{23} \\ 2 & a_{32} & a_{33}\end{array}\right| = 2 2 2 a 12 a 22 a 32 a 13 a 23 a 33 按照第一列展开= 2 A 11 + 2 A 21 + 2 A 31 = 3 =2 A_{11}+2 A_{21}+2 A_{31}=3 = 2 A 11 + 2 A 21 + 2 A 31 = 3 则答案:A 11 + A 21 + A 31 = 3 2 A_{11}+A_{21}+A_{31}=\frac{3}{2} A 11 + A 21 + A 31 = 2 3 用元素和代数余子式的乘积这条路走不通,计算量太大[ 分析 ] A i j → 概念 。 \displaystyle \begin{aligned} & {[\text { 分析 }] A_{i j} \rightarrow \text { 概念 。 }} \end{aligned} [ 分析 ] A ij → 概念 。 → 定理 { ∣ A ∣ = a 11 A 11 + a 12 A 12 + ⋯ + a 1 n A 1 n a 11 A 21 + a 12 A 22 + ⋯ + a 1 n A 2 n = 0 \displaystyle \begin{aligned} \rightarrow \text { 定理 }\left\{\begin{array}{l}|A|=a_{11} A_{11}+a_{12} A_{12}+\cdots+a_{1 n} A_{1 n} \\a_{11} A_{21}+a_{12} A_{22}+\cdots+a_{1 n} A_{2 n}=0\end{array}\right. \end{aligned} → 定理 { ∣ A ∣ = a 11 A 11 + a 12 A 12 + ⋯ + a 1 n A 1 n a 11 A 21 + a 12 A 22 + ⋯ + a 1 n A 2 n = 0 方法3: A的每行元素之和为2,说明2是一个特征值,(1,1,1)ᵀ是一个特征向量 A [ 1 1 1 ] = [ 2 2 2 ] = 2 [ 1 1 1 ] \displaystyle A\left[\begin{array}{l}1 \\ 1 \\ 1\end{array}\right]=\left[\begin{array}{l}2 \\ 2 \\ 2\end{array}\right]=2\left[\begin{array}{l}1 \\ 1 \\ 1\end{array}\right] A 1 1 1 = 2 2 2 = 2 1 1 1 ∣ A ∣ = 3 |A|=3 ∣ A ∣ = 3 代数余子式的两个角度 从伴随矩阵分析(对应方法一) 从行列式的展开分析(对应方法二) 接下来用伴随矩阵分析 ∇ \nabla ∇ 当 A ∗ = [ ( A 11 A 21 A 31 A 12 A 22 A 32 A 13 A 23 A 33 ] \displaystyle A^*=\left[\begin{array}{}\left(A_{11}\right. & A_{21} & A_{31} \\ A_{12} & A_{22} & A_{32} \\ A_{13} & A_{23} & A_{33}\end{array}\right] A ∗ = ( A 11 A 12 A 13 A 21 A 22 A 23 A 31 A 32 A 33 要求的是 则伴随矩阵第1,2,3行的和可以写为A ∗ [ 1 1 1 ] = [ ( 1 = A 11 + A 21 + A 31 = 3 2 ) ( 2 ) ( 3 ) ] \displaystyle A^*\left[\begin{array}{l}1 \\ 1 \\ 1\end{array}\right]=\left[\begin{array}{l}(1=A_{11}+A_{21}+A_{31}=\frac{3}{2}) \\ (2) \\ (3)\end{array}\right] A ∗ 1 1 1 = ( 1 = A 11 + A 21 + A 31 = 2 3 ) ( 2 ) ( 3 ) ∇ \nabla ∇ A A A { a 11 + a 12 + a 13 = 2 a 21 + a 22 + a 23 = 2 a 31 + a 32 + a 33 = 2 \displaystyle \left\{\begin{array}{l}a_{11}+a_{12}+a_{13}=2 \\a_{21}+a_{22}+a_{23}=2 \\a_{31}+a_{32}+a_{33}=2\end{array}\right. ⎩ ⎨ ⎧ a 11 + a 12 + a 13 = 2 a 21 + a 22 + a 23 = 2 a 31 + a 32 + a 33 = 2 这其实是一个乘法[ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] [ 1 1 1 ] = [ 2 2 2 ] → 将矩阵简写 A [ 1 1 1 ] = [ 2 2 2 ] \displaystyle \left[\begin{array}{lll}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{array}\right]\left[\begin{array}{l}1 \\1 \\1\end{array}\right]=\left[\begin{array}{l}2 \\2 \\2\end{array}\right]\xrightarrow[]{\text{将矩阵简写}}A\left[\begin{array}{l}1 \\ 1 \\ 1\end{array}\right]=\left[\begin{array}{l}2 \\ 2 \\ 2\end{array}\right] a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 1 1 1 = 2 2 2 将矩阵简写 A 1 1 1 = 2 2 2 另一种写法,A [ 1 1 1 ] = [ 2 2 2 ] → 用 A ∗ 左乘 \displaystyle A\left[\begin{array}{l}1 \\ 1 \\ 1\end{array}\right]=\left[\begin{array}{l}2 \\ 2 \\ 2\end{array}\right]\xrightarrow[]{\text{用}A^*\text{左乘}} A 1 1 1 = 2 2 2 用 A ∗ 左乘 A ∗ [ 2 2 2 ] = A ∗ A ‾ [ 1 1 1 ] → A ∗ ⋅ A = ∣ A ∣ ∣ A ∣ E [ 1 1 1 ] = 3 [ 1 1 1 ] A^*\left[\begin{array}{l}2 \\2 \\2\end{array}\right]=\underline{A^* A}\left[\begin{array}{l}1 \\1 \\1\end{array}\right]\xrightarrow[]{A^{*}\cdot A=|A|}|A| E\left[\begin{array}{l}1 \\1 \\1\end{array}\right]=3\left[\begin{array}{l}1 \\1 \\1\end{array}\right] A ∗ 2 2 2 = A ∗ A 1 1 1 A ∗ ⋅ A = ∣ A ∣ ∣ A ∣ E 1 1 1 = 3 1 1 1 式子两边倍除2,得到∴ A ∗ [ 1 1 1 ] = [ 3 2 3 2 2 2 ] \displaystyle \therefore A^*\left[\begin{array}{l}1 \\ 1 \\ 1\end{array}\right]=\left[\begin{array}{l}\frac{3}{2} \\ \frac{3}{2} \\ \frac{2}{2}\end{array}\right] ∴ A ∗ 1 1 1 = 2 3 2 3 2 2 从而伴随矩阵的第一行元素:A 11 + A 21 + A 31 = 3 2 A_{11}+A_{21}+A_{31}=\frac{3}{2} A 11 + A 21 + A 31 = 2 3 (16) 甲、乙两个盒子中各装有 2 个红球和 2 个白球, 先从甲盒中任取一球, 观察颜色后放入乙盒, 再从乙盒中任取一球, 令 X , Y X, Y X , Y X X X Y Y Y
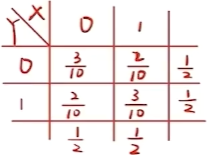
(16) (解) 根据相关系数的计算公式, X X X Y Y Y ρ = Cov ( X , Y ) D ( X ) D ( Y ) = E ( X Y ) − E ( X ) E ( Y ) D ( X ) D ( Y ) . \rho=\frac{\operatorname{Cov}(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}=\frac{E(X Y)-E(X) E(Y)}{\sqrt{D(X)} \sqrt{D(Y)}} . ρ = D ( X ) D ( Y ) Cov ( X , Y ) = D ( X ) D ( Y ) E ( X Y ) − E ( X ) E ( Y ) . P { X = 0 ⋅ Y = 0 } = 2 4 ⋅ 3 5 = 3 10 \displaystyle P\{X=0 \cdot Y=0\} =\frac{2}{4} \cdot \frac{3}{5}=\frac{3}{10} P { X = 0 ⋅ Y = 0 } = 4 2 ⋅ 5 3 = 10 3 P { X = 1 , Y = 0 } = 2 4 ⋅ 2 5 = 2 10 \displaystyle P\{X=1, Y=0\}=\frac{2}{4} \cdot \frac{2}{5}=\frac{2}{10} P { X = 1 , Y = 0 } = 4 2 ⋅ 5 2 = 10 2 P { X = 0 ⋅ Y = 1 } = 2 4 ⋅ 2 5 = 2 10 \displaystyle P\{X=0 \cdot Y=1\}=\frac{2}{4} \cdot \frac{2}{5}=\frac{2}{10} P { X = 0 ⋅ Y = 1 } = 4 2 ⋅ 5 2 = 10 2 P { X = 1 , Y = 1 } = 2 4 ⋅ 3 5 = 3 10 \displaystyle P\{X=1, Y=1\}=\frac{2}{4} \cdot \frac{3}{5}=\frac{3}{10} P { X = 1 , Y = 1 } = 4 2 ⋅ 5 3 = 10 3 下面分别计算 X , Y X, Y X , Y 从甲盒中取到红球的概率X X X X = 0 X=0 X = 0 X = 1 X=1 X = 1 P { X = 0 } = 1 2 , P { X = 1 } = 1 2 . P\{X=0\}=\frac{1}{2}, \quad P\{X=1\}=\frac{1}{2} . P { X = 0 } = 2 1 , P { X = 1 } = 2 1 . E ( X ) = 0 × 1 2 + 1 × 1 2 = 1 2 E(X)=0 \times \frac{1}{2}+1 \times \frac{1}{2}=\frac{1}{2} E ( X ) = 0 × 2 1 + 1 × 2 1 = 2 1 E ( X 2 ) = 0 × 1 2 + 1 2 × 1 2 = 1 2 E(X^2)=0 \times \frac{1}{2}+1^2 \times \frac{1}{2}=\frac{1}{2} E ( X 2 ) = 0 × 2 1 + 1 2 × 2 1 = 2 1 D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 = 1 2 − ( 1 2 ) 2 = 1 4 \displaystyle D(X)=E(X^2)-[E(X)]^2=\frac{1}{2}-\left(\frac{1}{2}\right)^2=\frac{1}{4} D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 = 2 1 − ( 2 1 ) 2 = 4 1 从乙盒中取到红球的概率Y Y Y 分析Y的概率 若从甲盒中取出的是白球, 则后来乙盒中共有 2 个红球和 3 个白球, 取到红球的概率为 2 5 \frac{2}{5} 5 2 即在 X = 0 X=0 X = 0 Y = 1 Y=1 Y = 1 2 5 \frac{2}{5} 5 2 若从甲盒中取出的是红球, 则后来乙盒中共有 3 个红球和 2 个白球, 取到红球的概率为 3 5 \frac{3}{5} 5 3 即在 X = 1 X=1 X = 1 Y = 1 Y=1 Y = 1 3 5 \frac{3}{5} 5 3 P { Y = 0 } = 1 2 , P { Y = 1 } = 1 2 . \displaystyle P\{Y=0\}=\frac{1}{2}, \quad P\{Y=1\}=\frac{1}{2} . P { Y = 0 } = 2 1 , P { Y = 1 } = 2 1 . P { Y = 1 } = P { Y = 1 ∣ X = 0 } P { X = 0 } + P { Y = 1 ∣ X = 1 } P { X = 1 } \displaystyle P\{Y=1\} =P\{Y=1 \mid X=0\} P\{X=0\}+P\{Y=1 \mid X=1\} P\{X=1\} P { Y = 1 } = P { Y = 1 ∣ X = 0 } P { X = 0 } + P { Y = 1 ∣ X = 1 } P { X = 1 } = 2 5 × 1 2 + 3 5 × 1 2 = 1 2 \displaystyle =\frac{2}{5} \times \frac{1}{2}+\frac{3}{5} \times \frac{1}{2}=\frac{1}{2} = 5 2 × 2 1 + 5 3 × 2 1 = 2 1 P { Y = 0 } = 1 − P { Y = 1 } = 1 − 1 2 = 1 2 . P\{Y=0\}=1-P\{Y=1\}=1-\frac{1}{2}=\frac{1}{2} . P { Y = 0 } = 1 − P { Y = 1 } = 1 − 2 1 = 2 1 . 同理, E ( Y ) = 1 2 , E ( Y 2 ) = 1 2 , D ( Y ) = 1 2 − ( 1 2 ) 2 = 1 4 E(Y)=\frac{1}{2}, E\left(Y^2\right)=\frac{1}{2}, D(Y)=\frac{1}{2}-\left(\frac{1}{2}\right)^2=\frac{1}{4} E ( Y ) = 2 1 , E ( Y 2 ) = 2 1 , D ( Y ) = 2 1 − ( 2 1 ) 2 = 4 1 X Y X Y X Y P { X Y = 1 } = P { X = 1 , Y = 1 } = P { Y = 1 ∣ X = 1 } P { X = 1 } = 3 5 × 1 2 = 3 10 . \displaystyle P\{X Y=1\}=P\{X=1, Y=1\}=P\{Y=1 \mid X=1\} P\{X=1\}=\frac{3}{5} \times \frac{1}{2}=\frac{3}{10} . P { X Y = 1 } = P { X = 1 , Y = 1 } = P { Y = 1 ∣ X = 1 } P { X = 1 } = 5 3 × 2 1 = 10 3 . P { X Y = 0 } = 1 − 3 10 = 7 10 . \displaystyle P\{X Y=0\}=1-\frac{3}{10}=\frac{7}{10} . P { X Y = 0 } = 1 − 10 3 = 10 7 . 于是, E ( X Y ) = P { X Y = 1 } × 1 + P { X Y = 0 } × 0 E(X Y)=P\{X Y=1\} \times 1+P\{X Y=0\} \times 0 E ( X Y ) = P { X Y = 1 } × 1 + P { X Y = 0 } × 0 = 3 10 × 1 + 7 16 × 0 = 3 10 \displaystyle =\frac{3}{10} \times 1+\frac{7}{16} \times 0=\frac{3}{10} = 10 3 × 1 + 16 7 × 0 = 10 3 因此,ρ = E ( X Y ) − E ( X ) E ( Y ) D ( X ) D ( Y ) = 3 10 − 1 2 × 1 2 1 2 × 1 2 = 1 20 1 4 = 1 5 . \displaystyle \rho=\frac{E(X Y)-E(X) E(Y)}{\sqrt{D(X)} \sqrt{D(Y)}}=\frac{\frac{3}{10}-\frac{1}{2} \times \frac{1}{2}}{\frac{1}{2} \times \frac{1}{2}}=\frac{\frac{1}{20}}{\frac{1}{4}}=\frac{1}{5} . ρ = D ( X ) D ( Y ) E ( X Y ) − E ( X ) E ( Y ) = 2 1 × 2 1 10 3 − 2 1 × 2 1 = 4 1 20 1 = 5 1 . 三、解答题 (本题共 6 小题, 共 70 分, 解答应写出文字说明、证明过程或演算步骤.)
(17) (本题满分 10 分)lim x → 0 ( 1 + ∫ 0 x e t 2 d t e x − 1 − 1 sin x ) \displaystyle \lim _{x \rightarrow 0}\left(\frac{1+\int_{0}^{x} \mathrm{e}^{t^{2}} \mathrm{~d} t}{\mathrm{e}^{x}-1}-\frac{1}{\sin x}\right) x → 0 lim ( e x − 1 1 + ∫ 0 x e t 2 d t − sin x 1 )
(17) 原式 = lim x → 0 sin x + sin x ∫ 0 x e t 2 d t − e x + 1 ( e x − 1 ) sin x → e x − 1 ∼ x sin x ∼ x } x 2 \displaystyle = \lim_{x \to 0} \frac{\sin x + \sin x \int_0^x e^{t^2} dt - e^x + 1}{ (e^x - 1) \sin x} \xrightarrow[]{\left.\begin{array}{l}e^x-1 \sim x \\\sin x \sim x\end{array}\right\} x^2} = x → 0 lim ( e x − 1 ) sin x sin x + sin x ∫ 0 x e t 2 d t − e x + 1 e x − 1 ∼ x sin x ∼ x } x 2 = 乘法求导 洛必达 lim x → 0 cos x + cos x ∫ 0 x e t 2 d t + sin x ⋅ e x 2 − e x 2 x \displaystyle \xlongequal[\text{乘法求导}]{\text{洛必达}}\lim_{x \to 0} \frac{\cos x + \cos x \int_0^x e^{t^2} dt + \sin x \cdot e^{x^2} - e^x}{2x} 洛必达 乘法求导 x → 0 lim 2 x cos x + cos x ∫ 0 x e t 2 d t + sin x ⋅ e x 2 − e x = 就洛必达几次 分母有几次 lim x → 0 − sin x − sin x ∫ 0 x e t 2 d t + cos x ⋅ e x 2 + cos x ⋅ e x 2 + sin x ⋅ e x 2 ⋅ 2 x − e x 2 \displaystyle \xlongequal[\text{就洛必达几次}]{\text{分母有几次}} \lim_{x \to 0} \frac{-\sin x - \sin x \int_0^x e^{t^2} dt + \cos x \cdot e^{x^2} + \cos x \cdot e^{x^2} + \sin x \cdot e^{x^2} \cdot 2x - e^x}{2} 分母有几次 就洛必达几次 x → 0 lim 2 − sin x − sin x ∫ 0 x e t 2 d t + cos x ⋅ e x 2 + cos x ⋅ e x 2 + sin x ⋅ e x 2 ⋅ 2 x − e x = sin 0 = 0 , cos 0 = 1 1 2 . \displaystyle \xlongequal[]{\sin 0=0, \cos 0=1} \frac{1}{2}. s i n 0 = 0 , c o s 0 = 1 2 1 . (18) (本题满分 12 分)u n ( x ) = e − n x + x n + 1 n ( n + 1 ) ( n = 1 , 2 , ⋯ ) u_{n}(x)=\mathrm{e}^{-n x}+\frac{x^{n+1}}{n(n+1)}(n=1,2, \cdots) u n ( x ) = e − n x + n ( n + 1 ) x n + 1 ( n = 1 , 2 , ⋯ ) ∑ n = 1 ∞ u n ( x ) \displaystyle \sum_{n=1}^{\infty} u_{n}(x) n = 1 ∑ ∞ u n ( x )
(18) 设 u n ( x ) = e − n x + x n + 1 n ( n + 1 ) \displaystyle u_n(x) = e^{-nx} + \frac{x^{n+1}}{n(n+1)} u n ( x ) = e − n x + n ( n + 1 ) x n + 1 n = 1 , 2 , ⋯ \displaystyle n = 1, 2, \cdots n = 1 , 2 , ⋯ ∑ n = 1 ∞ u n ( x ) \displaystyle \sum_{n=1}^{\infty} u_n(x) n = 1 ∑ ∞ u n ( x ) S ( x ) = ∑ n = 1 ∞ [ e − n x + 1 n ( n + 1 ) x n + 1 ] \displaystyle S(x) = \sum_{n=1}^{\infty} \left[ e^{-nx} + \frac{1}{n(n+1)} x^{n+1} \right] S ( x ) = n = 1 ∑ ∞ [ e − n x + n ( n + 1 ) 1 x n + 1 ] = ∑ n = 1 ∞ e − n x + ∑ n = 1 ∞ 1 n ( n + 1 ) x n + 1 \displaystyle = \sum_{n=1}^{\infty} e^{-nx} + \sum_{n=1}^{\infty} \frac{1}{n(n+1)} x^{n+1} = n = 1 ∑ ∞ e − n x + n = 1 ∑ ∞ n ( n + 1 ) 1 x n + 1 求收敛域 ∑ n = 1 ∞ e − n x = e − x + e − 2 x + ⋯ + e − n x + ⋯ = e − x 1 − e − x , − 1 < e − x < 1 , \displaystyle \sum_{n=1}^{\infty} e^{-nx} = e^{-x} + e^{-2x} + \cdots + e^{-nx} + \cdots = \frac{e^{-x}}{1 - e^{-x}}, \quad -1 < e^{-x} < 1, n = 1 ∑ ∞ e − n x = e − x + e − 2 x + ⋯ + e − n x + ⋯ = 1 − e − x e − x , − 1 < e − x < 1 , x > 0. x > 0. x > 0. 而∑ n = 1 ∞ x n + 1 n ( n + 1 ) , \displaystyle \sum_{n=1}^{\infty} \frac{x^{n+1}}{n(n+1)}, n = 1 ∑ ∞ n ( n + 1 ) x n + 1 , lim n → ∞ a n + 1 a n = lim n → ∞ n ( n + 1 ) ( n + 1 ) ( n + 2 ) = 1 , \lim_{n \to \infty} \frac{a_{n+1}}{a_n} = \lim_{n \to \infty} \frac{n(n+1)}{(n+1)(n+2)} = 1, lim n → ∞ a n a n + 1 = lim n → ∞ ( n + 1 ) ( n + 2 ) n ( n + 1 ) = 1 , R = 1. R = 1. R = 1. 又 x = 1 \displaystyle x = 1 x = 1 x = − 1 \displaystyle x = -1 x = − 1 ∑ n = 1 ∞ 1 n ( n + 1 ) \displaystyle \sum_{n=1}^{\infty} \frac{1}{n(n+1)} n = 1 ∑ ∞ n ( n + 1 ) 1 ∑ n = 1 ∞ ( − 1 ) n + 1 n ( n + 1 ) \displaystyle \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n(n+1)} n = 1 ∑ ∞ n ( n + 1 ) ( − 1 ) n + 1 所以 ∑ n = 1 ∞ x n + 1 n ( n + 1 ) \displaystyle \sum_{n=1}^{\infty} \frac{x^{n+1}}{n(n+1)} n = 1 ∑ ∞ n ( n + 1 ) x n + 1 [ − 1 , 1 ] [-1, 1 ] [ − 1 , 1 ] 所以级数 ∑ n = 1 ∞ u n ( x ) \displaystyle \sum_{n=1}^{\infty} u_n(x) n = 1 ∑ ∞ u n ( x ) ( 0 , 1 ] \displaystyle (0,1] ( 0 , 1 ] S ( x ) = ∑ n = 1 ∞ x n + 1 n ( n + 1 ) \displaystyle S(x) = \sum_{n=1}^{\infty} \frac{x^{n+1}}{n(n+1)} S ( x ) = n = 1 ∑ ∞ n ( n + 1 ) x n + 1 0 < x ≤ 1 \displaystyle 0 < x \leq 1 0 < x ≤ 1 求和函数S ( x ) = ∑ n = 1 ∞ e − n x + ∑ n = 1 ∞ 1 n ( n + 1 ) x n + 1 \displaystyle S(x)= \sum_{n=1}^{\infty} e^{-nx} + \sum_{n=1}^{\infty} \frac{1}{n(n+1)} x^{n+1} S ( x ) = n = 1 ∑ ∞ e − n x + n = 1 ∑ ∞ n ( n + 1 ) 1 x n + 1 第一部分 ∑ n = 1 ∞ e − n x = ∑ n = 1 ∞ t n , − 1 < t < 1 → ∑ n = 0 ∞ x n = 1 1 − x e − x 1 − e − x \displaystyle \sum_{n=1}^{\infty} e^{-nx} = \sum_{n=1}^{\infty} t^n, \quad -1 < t < 1 \xrightarrow[]{\sum_{n=0}^{\infty} x^n=\frac{1}{1-x}}\frac{e^{-x}}{1 - e^{-x}} n = 1 ∑ ∞ e − n x = n = 1 ∑ ∞ t n , − 1 < t < 1 ∑ n = 0 ∞ x n = 1 − x 1 1 − e − x e − x 第二部分 逐项求导 当 0 < x < 1 \displaystyle 0 < x < 1 0 < x < 1 S ′ ( x ) = ∑ n = 1 ∞ x n n = − ln ( 1 − x ) \displaystyle S'(x) = \sum_{n=1}^{\infty} \frac{x^n}{n} = -\ln(1-x) S ′ ( x ) = n = 1 ∑ ∞ n x n = − ln ( 1 − x ) ln ( 1 + x ) = ∑ n = 1 ∞ ( − 1 ) n − 1 x n n \displaystyle \ln(1+x) = \sum_{n=1}^{\infty} \frac{(-1)^{n-1} x^n}{n} ln ( 1 + x ) = n = 1 ∑ ∞ n ( − 1 ) n − 1 x n − 1 < x < 1 \displaystyle -1 < x < 1 − 1 < x < 1 逐项积分 \displaystyle S ( x ) = ∫ 0 x − ln ( 1 − t ) d t + S ( 0 ) = − t ln ( 1 − t ) ∣ 0 x + ∫ 0 x t ⋅ − 1 1 − t d t + 0 S(x) = \int_0^x -\ln(1-t) \, dt + S(0) = -t\ln(1-t) \bigg|_0^x + \int_0^x t \cdot \frac{-1}{1-t} \, dt + 0 S ( x ) = ∫ 0 x − ln ( 1 − t ) d t + S ( 0 ) = − t ln ( 1 − t ) 0 x + ∫ 0 x t ⋅ 1 − t − 1 d t + 0 = − x ln ( 1 − x ) + ∫ 0 x 1 − t − 1 1 − t d t = − x ln ( 1 − x ) + x + ln ( 1 − x ) . \displaystyle = -x\ln(1-x) + \int_0^x \frac{1-t-1}{1-t} \, dt = -x\ln(1-x) + x + \ln(1-x). = − x ln ( 1 − x ) + ∫ 0 x 1 − t 1 − t − 1 d t = − x ln ( 1 − x ) + x + ln ( 1 − x ) . 补点:而 S ( x ) \displaystyle S(x) S ( x ) S ( 1 ) = lim x → 1 S ( x ) \displaystyle S(1) = \lim_{x \to 1} S(x) S ( 1 ) = x → 1 lim S ( x ) = lim x → 1 − [ − x ln ( 1 − x ) + x + ln ( 1 − x ) ] \displaystyle = \lim_{x \to 1^-} \left[ -x\ln(1-x) + x + \ln(1-x) \right] = x → 1 − lim [ − x ln ( 1 − x ) + x + ln ( 1 − x ) ] = lim x → 1 − ( 1 − x ) ⏟ = 0 ln ( 1 − x ) + 1 \displaystyle = \lim_{x \to 1^-} \underbrace{(1-x)}_{=0}\ln(1-x) + 1 = x → 1 − lim = 0 ( 1 − x ) ln ( 1 − x ) + 1 (令 1 − x = t \displaystyle 1-x = t 1 − x = t = lim t → 0 + t ln t + 1 = 0 + 1 = 1 \displaystyle = \lim_{t \to 0^+} t\ln t + 1 = 0 + 1 = 1 = t → 0 + lim t ln t + 1 = 0 + 1 = 1 综上可知,级数 ∑ n = 1 ∞ u n ( x ) \displaystyle \sum_{n=1}^{\infty} u_n(x) n = 1 ∑ ∞ u n ( x ) { e − x 1 − e − x − x ln ( 1 − x ) + x + ln ( 1 − x ) , 0 < x < 1 , e − 1 1 − e − 1 + 1 , x = 1. \displaystyle \begin{cases}\frac{e^{-x}}{1-e^{-x}} - x\ln(1-x) + x + \ln(1-x), 0 < x < 1, \\\frac{e^{-1}}{1-e^{-1}} + 1, x = 1.\end{cases} { 1 − e − x e − x − x ln ( 1 − x ) + x + ln ( 1 − x ) , 0 < x < 1 , 1 − e − 1 e − 1 + 1 , x = 1. 小猪佩奇 1 n ⋅ ( n + 1 ) = 1 n − 1 n + 1 \displaystyle \frac{1}{n \cdot (n+1)} = \frac{1}{n} - \frac{1}{n+1} n ⋅ ( n + 1 ) 1 = n 1 − n + 1 1 ∑ n = 1 ∞ 1 n ( n + 1 ) x n + 1 \displaystyle \sum_{n=1}^{\infty} \frac{1}{n(n+1)} x^{n+1} n = 1 ∑ ∞ n ( n + 1 ) 1 x n + 1 = 裂项 ∑ n = 1 ∞ [ x n + 1 n − 1 n + 1 x n + 1 ] \displaystyle \xlongequal[]{\text{裂项}}\sum_{n=1}^{\infty} \left[ \frac{x^{n+1}}{n} - \frac{1}{n+1} x^{n+1} \right] 裂项 n = 1 ∑ ∞ [ n x n + 1 − n + 1 1 x n + 1 ] = 向分母看齐 x ∑ n = 1 ∞ x n n − ∑ n = 1 ∞ x n + 1 n + 1 \displaystyle \xlongequal[]{\text{向分母看齐}}x \sum_{n=1}^{\infty} \frac{x^n}{n} - \sum_{n=1}^{\infty} \frac{x^{n+1}}{n+1} 向分母看齐 x n = 1 ∑ ∞ n x n − n = 1 ∑ ∞ n + 1 x n + 1 = 套公式 x ⋅ [ − ln ( 1 − x ) ] + ln ( 1 − x ) + x \displaystyle \xlongequal[]{\text{套公式}} x \cdot[-\ln(1-x)] + \ln(1-x) + x 套公式 x ⋅ [ − ln ( 1 − x )] + ln ( 1 − x ) + x = 合并同类项 ( 1 − x ) ⋅ ln ( 1 − x ) + x \displaystyle \xlongequal[]{\text{合并同类项}} (1-x) \cdot \ln(1-x) + x 合并同类项 ( 1 − x ) ⋅ ln ( 1 − x ) + x (19) (本题满分 12 分)C : { x 2 + 2 y 2 − z = 6 , 4 x + 2 y + z = 30 , \displaystyle C:\left\{\begin{array}{l}x^{2}+2 y^{2}-z=6, \\ 4 x+2 y+z=30,\end{array}\right. C : { x 2 + 2 y 2 − z = 6 , 4 x + 2 y + z = 30 , C C C x O y x O y x O y
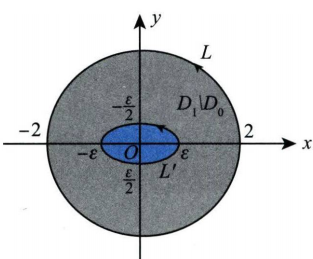
(19) 分析 本题可以利用拉格朗日乘数法求解.点 ( x , y , z ) (x, y, z) ( x , y , z ) x O y x O y x O y ∣ z ∣ |z| ∣ z ∣ z 2 z^2 z 2 ( x , y , z ) (x, y, z) ( x , y , z ) C C C → 建立拉格朗日函数 L ( x , y , z , λ , μ ) = ∣ z ∣ + λ ( x 2 + 2 y 2 − z − 6 ) + μ ( 4 x + 2 y + z − 30 ) \xrightarrow[]{\text{建立拉格朗日函数}}L(x, y, z, \lambda, \mu)=|z|+\lambda\left(x^2+2 y^2-z-6\right)+\mu(4 x+2 y+z-30) 建立拉格朗日函数 L ( x , y , z , λ , μ ) = ∣ z ∣ + λ ( x 2 + 2 y 2 − z − 6 ) + μ ( 4 x + 2 y + z − 30 ) → 绝对值变成平方 L ( x , y , z , λ , μ ) = z 2 + λ ( x 2 + 2 y 2 − z − 6 ) + μ ( 4 x + 2 y + z − 30 ) \displaystyle \begin{aligned} \xrightarrow[]{\text{绝对值变成平方}} L(x, y, z, \lambda, \mu)=z^2+\lambda\left(x^2+2 y^2-z-6\right)+\mu(4 x+2 y+z-30) \end{aligned} 绝对值变成平方 L ( x , y , z , λ , μ ) = z 2 + λ ( x 2 + 2 y 2 − z − 6 ) + μ ( 4 x + 2 y + z − 30 ) { ( 1 ) L x = 2 λ x + 4 μ = 0 ( 2 ) L y = 4 λ y + 2 μ = 0 ( 3 ) L z = 2 z − λ + μ = 0 ( 4 ) L λ = x 2 + 2 y 2 − z − 6 = 0 ( 5 ) L μ = 4 x + 2 y + z − 30 = 0 \displaystyle \begin{aligned} \left\{\begin{array}{l}(1)L_x=2 \lambda x+4 \mu=0 \\(2)L_y=4 \lambda y+2 \mu=0 \\(3)L_z=2 z-\lambda+\mu=0 \\(4)L_\lambda=x^2+2 y^2-z-6=0 \\(5)L_\mu=4 x+2 y+z-30=0\end{array}\right. \end{aligned} ⎩ ⎨ ⎧ ( 1 ) L x = 2 λ x + 4 μ = 0 ( 2 ) L y = 4 λ y + 2 μ = 0 ( 3 ) L z = 2 z − λ + μ = 0 ( 4 ) L λ = x 2 + 2 y 2 − z − 6 = 0 ( 5 ) L μ = 4 x + 2 y + z − 30 = 0 gpt版 转化问题:求 C C C x O y xOy x O y z z z 曲线 C C C { x 2 + 2 y 2 − z = 6 , 4 x + 2 y + z = 30 } \{x^2 + 2y^2 - z = 6, 4x + 2y + z = 30\} { x 2 + 2 y 2 − z = 6 , 4 x + 2 y + z = 30 } 构造拉格朗日函数 L ( x , y , z , λ , μ ) L(x, y, z, \lambda, \mu) L ( x , y , z , λ , μ ) L ( x , y , z , λ , μ ) = z + λ ( 4 x + 2 y + z − 30 ) + μ ( x 2 + 2 y 2 − z − 6 ) L(x, y, z, \lambda, \mu) = z + \lambda(4x + 2y + z - 30) + \mu(x^2 + 2y^2 - z - 6) L ( x , y , z , λ , μ ) = z + λ ( 4 x + 2 y + z − 30 ) + μ ( x 2 + 2 y 2 − z − 6 ) 消元法求解驻点:对 L L L ∂ L ∂ x = 4 λ + 2 μ x = 0 \frac{\partial L}{\partial x} = 4\lambda + 2\mu x = 0 ∂ x ∂ L = 4 λ + 2 μx = 0 ∂ L ∂ y = 2 λ + 4 μ y = 0 \frac{\partial L}{\partial y} = 2\lambda + 4\mu y = 0 ∂ y ∂ L = 2 λ + 4 μ y = 0 ∂ L ∂ z = 1 + λ − μ = 0 \frac{\partial L}{\partial z} = 1 + \lambda - \mu = 0 ∂ z ∂ L = 1 + λ − μ = 0 ∂ L ∂ λ = 4 x + 2 y + z − 30 = 0 \frac{\partial L}{\partial \lambda} = 4x + 2y + z - 30 = 0 ∂ λ ∂ L = 4 x + 2 y + z − 30 = 0 ∂ L ∂ μ = x 2 + 2 y 2 − z − 6 = 0 \frac{\partial L}{\partial \mu} = x^2 + 2y^2 - z - 6 = 0 ∂ μ ∂ L = x 2 + 2 y 2 − z − 6 = 0 消元法求解驻点的坐标。 解得两组解:( x , y , z ) = ( 4 , 1 , 12 ) (x, y, z) = (4, 1, 12) ( x , y , z ) = ( 4 , 1 , 12 ) ( − 8 , − 2 , 66 ) (-8, -2, 66) ( − 8 , − 2 , 66 ) 确定最大值。 (20) 设 D ⊂ R 2 D \subset \mathbf{R}^{2} D ⊂ R 2 I ( D ) = ∬ D ( 4 − x 2 − y 2 ) d x d y I(D)=\iint_{D}\left(4-x^{2}-y^{2}\right) \mathrm{d} x \mathrm{~d} y I ( D ) = ∬ D ( 4 − x 2 − y 2 ) d x d y D 1 D_{1} D 1 I ( D 1 ) I\left(D_{1}\right) I ( D 1 ) ∫ ∂ D 1 ( x e x 2 + 4 y 2 + y ) d x + ( 4 y e x 2 + 4 y 2 − x ) d y x 2 + 4 y 2 \displaystyle \int_{\partial D_{1}} \frac{\left(x \mathrm{e}^{x^{2}+4 y^{2}}+y\right) \mathrm{d} x+\left(4 y \mathrm{e}^{x^{2}+4 y^{2}}-x\right) \mathrm{d} y}{x^{2}+4 y^{2}} ∫ ∂ D 1 x 2 + 4 y 2 ( x e x 2 + 4 y 2 + y ) d x + ( 4 y e x 2 + 4 y 2 − x ) d y ∂ D 1 \partial D_{1} ∂ D 1 D 1 D_{1} D 1
(20) (1)区域 D 1 \displaystyle D_1 D 1 f ( x , y ) = 4 − x 2 − y 2 ≥ 0 \displaystyle f(x, y) = 4 - x^2 - y^2 \geq 0 f ( x , y ) = 4 − x 2 − y 2 ≥ 0 且 D 1 \displaystyle D_1 D 1 f ( x , y ) = 4 − x 2 − y 2 < 0 \displaystyle f(x, y) = 4 - x^2 - y^2 < 0 f ( x , y ) = 4 − x 2 − y 2 < 0 所以 D 1 = { ( x , y ) ∣ x 2 + y 2 ≤ 4 } \displaystyle D_1 = \{(x, y) | x^2 + y^2 \leq 4\} D 1 = {( x , y ) ∣ x 2 + y 2 ≤ 4 } I ( D 1 ) = ∬ D 1 ( 4 − x 2 − y 2 ) d x d y = ∫ 0 2 π d θ ∫ 0 2 ( 4 − r 2 ) r d r = ( 2 r 2 − r 4 4 ) ∣ 0 2 = 8 − 4 = 4 8 π . \displaystyle I(D_1) = \iint_{D_1} (4 - x^2 - y^2) \, dx \, dy = \int_0^{2\pi} d\theta \int_0^2 (4 - r^2) r \, dr \xlongequal[]{\left.\left(2 r^2-\frac{r^4}{4}\right)\right|_0 ^2=8-4=4}8\pi. I ( D 1 ) = ∬ D 1 ( 4 − x 2 − y 2 ) d x d y = ∫ 0 2 π d θ ∫ 0 2 ( 4 − r 2 ) r d r ( 2 r 2 − 4 r 4 ) 0 2 = 8 − 4 = 4 8 π . (2) 记所求积分为 I , P ( x , y ) = x e x 2 + 4 y 2 + y x 2 + 4 y 2 , Q ( x , y ) = 4 y e x 2 + 4 y 2 − x x 2 + 4 y 2 I, P(x, y)=\frac{x \mathrm{e}^{x^2+4 y^2}+y}{x^2+4 y^2}, Q(x, y)=\frac{4 y \mathrm{e}^{x^2+4 y^2}-x}{x^2+4 y^2} I , P ( x , y ) = x 2 + 4 y 2 x e x 2 + 4 y 2 + y , Q ( x , y ) = x 2 + 4 y 2 4 y e x 2 + 4 y 2 − x ( x , y ) ≠ ( 0 , 0 ) (x, y) \neq(0,0) ( x , y ) = ( 0 , 0 ) ∂ Q ∂ x = ( 8 x y e x 2 + 4 y 2 − 1 ) ( x 2 + 4 y 2 ) − ( 4 y e x 2 + 4 y 2 − x ) ⋅ 2 x ( x 2 + 4 y 2 ) 2 = ∂ P ∂ y \displaystyle \frac{\partial Q}{\partial x} =\frac{\left(8 x y \mathrm{e}^{x^2+4 y^2}-1\right)\left(x^2+4 y^2\right)-\left(4 y \mathrm{e}^{x^2+4 y^2}-x\right) \cdot 2 x}{\left(x^2+4 y^2\right)^2} =\frac{\partial P}{\partial y} ∂ x ∂ Q = ( x 2 + 4 y 2 ) 2 ( 8 x y e x 2 + 4 y 2 − 1 ) ( x 2 + 4 y 2 ) − ( 4 y e x 2 + 4 y 2 − x ) ⋅ 2 x = ∂ y ∂ P 于是, ∂ Q ∂ x = ∂ P ∂ y \displaystyle \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} ∂ x ∂ Q = ∂ y ∂ P 挖点用格林由格林公式,∮ L P d x + Q d y = ∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d σ \displaystyle \begin{aligned}\oint_L P d x+Q d y=\iint_D\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d \sigma\end{aligned} ∮ L P d x + Q d y = ∬ D ( ∂ x ∂ Q − ∂ y ∂ P ) d σ 挖点前的全部区域:∮ L + L ′ ( x e x 2 + 4 y 2 + y ) d x + ( 4 y e x 2 + 4 y 2 − x ) d y x 2 + 4 y 2 = 格林公式 ∬ D 1 \ D 0 0 d x d y = 0 , \displaystyle \oint_{L+L^{\prime}} \frac{\left(x \mathrm{e}^{x^2+4 y^2}+y\right) \mathrm{d} x+\left(4 y \mathrm{e}^{x^2+4 y^2}-x\right) \mathrm{d} y}{x^2+4 y^2} \xlongequal{\text{ 格林公式 }} \iint_{D_1 \backslash D_0} 0 \mathrm{~d} x \mathrm{~d} y=0, ∮ L + L ′ x 2 + 4 y 2 ( x e x 2 + 4 y 2 + y ) d x + ( 4 y e x 2 + 4 y 2 − x ) d y 格林公式 ∬ D 1 \ D 0 0 d x d y = 0 , 挖点后的区域∮ L = ∮ L + L ′ ‾ − ∮ L ′ 内 \displaystyle \oint_{L} =\underline{\oint_{L+L'}}-\oint_{L^{'\text{内}}} ∮ L = ∮ L + L ′ − ∮ L ′ 内 = 0 + ∮ L ′ 外 \displaystyle =0+\oint_{L^{'\text{外}}} = 0 + ∮ L ′ 外 = ∮ L ′ - ( x e x 2 + 4 y 2 + y ) d x + ( 4 y e x 2 + 4 y 2 − x ) d y x 2 + 4 y 2 \displaystyle =\oint_{L^{\prime\text{-}}} \frac{\left(x \mathrm{e}^{x^2+4 y^2}+y\right) \mathrm{d} x+\left(4 y \mathrm{e}^{x^2+4 y^2}-x\right) \mathrm{d} y}{x^2+4 y^2} = ∮ L ′ - x 2 + 4 y 2 ( x e x 2 + 4 y 2 + y ) d x + ( 4 y e x 2 + 4 y 2 − x ) d y = x 2 + 4 y 2 = ε 2 ε 2 ∮ L ′ ( x e ε 2 + y ) d x + ( 4 y e ε 2 − x ) d y \displaystyle \xlongequal[x^2+4 y^2=\varepsilon^2]{\varepsilon^2} \oint_{L^{\prime}}\left(x \mathrm{e}^{\varepsilon^2}+y\right) \mathrm{d} x+\left(4 y \mathrm{e}^{\varepsilon^2}-x\right) \mathrm{d} y ε 2 x 2 + 4 y 2 = ε 2 ∮ L ′ ( x e ε 2 + y ) d x + ( 4 y e ε 2 − x ) d y = 格林公式 1 ε 2 ∬ D 0 [ ∂ Q ∂ x − ∂ P ∂ y ] d x d y = 1 ε 2 ∬ D 0 ( − 1 − 1 ) d x d y \displaystyle \xlongequal{\text{ 格林公式 }} \frac{1}{\varepsilon^2} \iint_{D_0}\left[\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right] \mathrm{d} x \mathrm{~d} y=\frac{1}{\varepsilon^2} \iint_{D_0}(-1-1) \mathrm{d} x \mathrm{~d} y 格林公式 ε 2 1 ∬ D 0 [ ∂ x ∂ Q − ∂ y ∂ P ] d x d y = ε 2 1 ∬ D 0 ( − 1 − 1 ) d x d y = − 2 ε 2 ⋅ D 0 \displaystyle =-\frac{2}{\varepsilon^2} \cdot D_0 = − ε 2 2 ⋅ D 0 = π a b − 2 ε 2 × π × ε × ε 2 = − π . \xlongequal[]{\pi ab}-\frac{2}{\varepsilon^2} \times \pi \times \varepsilon \times \frac{\varepsilon}{2}=-\pi . πab − ε 2 2 × π × ε × 2 ε = − π . 2000 年数一试题 计算曲线积分 I = ∮ L x d y − y d x 4 x 2 + y 2 I=\oint_L \frac{x \mathrm{~d} y-y \mathrm{~d} x}{4 x^2+y^2} I = ∮ L 4 x 2 + y 2 x d y − y d x L L L ( 1 , 0 ) (1,0) ( 1 , 0 ) R R R ( R > 1 ) (R>1) ( R > 1 ) 2020 年数一试题 计算曲线积分 I = ∮ L 4 x − y 4 x 2 + y 2 d x + x + y 4 x 2 + y 2 d y I=\oint_L \frac{4 x-y}{4 x^2+y^2} \mathrm{~d} x+\frac{x+y}{4 x^2+y^2} \mathrm{~d} y I = ∮ L 4 x 2 + y 2 4 x − y d x + 4 x 2 + y 2 x + y d y L L L x 2 + y 2 = 2 x^2+y^2=2 x 2 + y 2 = 2 (21) (本题满分 12 分)A = ( a 1 − 1 1 a − 1 − 1 − 1 a ) \displaystyle \boldsymbol{A}=\left(\begin{array}{ccc}a & 1 & -1 \\ 1 & a & -1 \\ -1 & -1 & a\end{array}\right) A = a 1 − 1 1 a − 1 − 1 − 1 a P \boldsymbol{P} P P T A P \boldsymbol{P}^{\mathrm{T}} \boldsymbol{A P} P T AP C \boldsymbol{C} C C 2 = ( a + 3 ) E − A \boldsymbol{C}^{2}=(a+3) \boldsymbol{E}-\boldsymbol{A} C 2 = ( a + 3 ) E − A E \boldsymbol{E} E
(21) 解 (1) ∣ A − λ E ∣ = ∣ a − λ 1 − 1 1 a − λ − 1 − 1 − 1 a − λ ∣ = c 1 + c 3 ∣ a − λ − 1 1 − 1 0 a − λ − 1 a − λ − 1 − 1 a − λ ∣ \displaystyle |A-\lambda E|=\left|\begin{array}{ccc}a-\lambda & 1 & -1 \\ 1 & a-\lambda & -1 \\ -1 & -1 & a-\lambda\end{array}\right|\xlongequal[]{c1+c3}\left|\begin{array}{ccc}a-\lambda-1 & 1 & -1 \\ 0 & a-\lambda & -1 \\ a-\lambda-1 & -1 & a-\lambda\end{array}\right| ∣ A − λ E ∣ = a − λ 1 − 1 1 a − λ − 1 − 1 − 1 a − λ c 1 + c 3 a − λ − 1 0 a − λ − 1 1 a − λ − 1 − 1 − 1 a − λ = r 3 − r 1 ∣ a − λ − 1 1 − 1 0 a − λ − 1 0 − 2 a − λ + 1 ∣ \displaystyle \begin{aligned} \xlongequal[]{r3-r1}\left|\begin{array}{ccc}a-\lambda-1 & 1 & -1 \\0 & a-\lambda & -1 \\0 & -2 & a-\lambda+1\end{array}\right| \end{aligned} r 3 − r 1 a − λ − 1 0 0 1 a − λ − 2 − 1 − 1 a − λ + 1 = 按第一列展开 ( a − λ − 1 ) [ ( a − λ ) ( a − λ + 1 ) − 2 ] \displaystyle \begin{aligned} \xlongequal[]{\text{按第一列展开}}(a-\lambda-1)[(a-\lambda)(a-\lambda+1)-2]\end{aligned} 按第一列展开 ( a − λ − 1 ) [( a − λ ) ( a − λ + 1 ) − 2 ] = ( a − λ − 1 ) [ ( a − λ ) 2 + ( a − λ ) − 2 ] \displaystyle \begin{aligned}=(a-\lambda-1)\left[(a-\lambda)^2+(a-\lambda)-2\right]\end{aligned} = ( a − λ − 1 ) [ ( a − λ ) 2 + ( a − λ ) − 2 ] = t + 2 t − 1 ( a − λ − 1 ) [ a − λ + 2 ] [ a − λ − 1 ] \displaystyle \begin{aligned} \xlongequal[]{\begin{aligned}& t+2 \\& t-1\end{aligned}}(a-\lambda-1)[a-\lambda+2][a-\lambda-1] \end{aligned} t + 2 t − 1 ( a − λ − 1 ) [ a − λ + 2 ] [ a − λ − 1 ] λ 1 = λ 2 = a − 1. λ 3 = a + 2 \lambda_1=\lambda_2=a-1 . \quad \lambda_3=a+2 λ 1 = λ 2 = a − 1. λ 3 = a + 2 当二重根λ = a − 1 \displaystyle \begin{aligned} \begin{gathered}\lambda=a-1 \end{gathered} \end{aligned} λ = a − 1 ( A − ( a − 1 ) E ) x = 0 \displaystyle \begin{aligned}(A-(a-1) E) x=0 \end{aligned} ( A − ( a − 1 ) E ) x = 0 ( 1 1 − 1 1 1 − 1 − 1 − 1 1 ) → 2 , 3 两行成比例 ( 1 1 − 1 0 0 0 0 0 0 ) \displaystyle \begin{aligned}\left(\begin{array}{ccc}1 & 1 & -1 \\1 & 1 & -1 \\-1 & -1 & 1\end{array}\right) \xrightarrow[]{2\text{,}3\text{两行成比例}}\left(\begin{array}{ccc}1 & 1 & -1 \\0 & 0 & 0 \\0 & 0 & 0\end{array}\right)\end{aligned} 1 1 − 1 1 1 − 1 − 1 − 1 1 2 , 3 两行成比例 1 0 0 1 0 0 − 1 0 0 x = k 1 ( − 1 1 0 ) + k 2 ( 1 0 1 ) \displaystyle x=k_1\left(\begin{array}{c}-1 \\1 \\0\end{array}\right)+k_2\left(\begin{array}{l}1 \\0 \\1\end{array}\right) x = k 1 − 1 1 0 + k 2 1 0 1 k 1 k_1 k 1 k 2 k_2 k 2 0 0 0 \displaystyle λ = a + 2 \lambda=a+2 λ = a + 2 ( A − ( a + 2 ) E ) x = 0 (A-(a+2) E) x=0 ( A − ( a + 2 ) E ) x = 0 → ( − 2 1 − 1 1 − 2 − 1 − 1 − 1 − 2 ) → 行互换化简 ( 1 1 2 1 − 2 − 1 − 2 1 − 1 ) \displaystyle \begin{aligned} \xrightarrow[]{} \left(\begin{array}{ccc}-2 & 1 & -1 \\1 & -2 & -1 \\-1 & -1 & -2\end{array}\right) \xrightarrow[]{\text{行互换化简}}\left(\begin{array}{ccc}1 & 1 & 2 \\1 & -2 & -1 \\-2 & 1 & -1\end{array}\right) \end{aligned} − 2 1 − 1 1 − 2 − 1 − 1 − 1 − 2 行互换化简 1 1 − 2 1 − 2 1 2 − 1 − 1 → r 2 − r 1 r 3 + 2 r 1 ( 1 1 2 0 − 3 − 3 0 3 3 ) → 2 , 3 两行成比例 ( 1 0 1 0 1 1 0 0 0 ) \displaystyle \begin{aligned}\xrightarrow[]{\begin{aligned}& r_2-r_1 \\& r_3+2 r_1\end{aligned}}\left(\begin{array}{ccc}1 & 1 & 2 \\0 & -3 & -3 \\0 & 3 & 3\end{array}\right) \xrightarrow[]{2\text{,}3\text{两行成比例}}\left(\begin{array}{lll}1 & 0 & 1 \\0 & 1 & 1 \\0 & 0 & 0\end{array}\right)\end{aligned} r 2 − r 1 r 3 + 2 r 1 1 0 0 1 − 3 3 2 − 3 3 2 , 3 两行成比例 1 0 0 0 1 0 1 1 0 ∴ x = k 3 ( − 1 − 1 1 ) \displaystyle \begin{aligned} \therefore x=k_3\left(\begin{array}{c}-1 \\-1 \\1\end{array}\right)\end{aligned} ∴ x = k 3 − 1 − 1 1 先施密特正交化 β 1 = ξ 1 = ( − 1 1 0 ) , \displaystyle \begin{aligned} \boldsymbol{\beta}_1=\boldsymbol{\xi}_1=\left(\begin{array}{c}-1 \\1 \\0\end{array}\right), \end{aligned} β 1 = ξ 1 = − 1 1 0 , β 2 = ξ 2 − ( β 1 , ξ 2 ) ∥ β 1 ∥ 2 β 1 = ( 1 0 1 ) − ( − 1 ) 2 ( − 1 1 0 ) = 1 2 ( 1 1 2 ) , \displaystyle \begin{aligned} \boldsymbol{\beta}_2=\boldsymbol{\xi}_2-\frac{\left(\boldsymbol{\beta}_1, \boldsymbol{\xi}_2\right)}{\left\|\boldsymbol{\beta}_1\right\|^2} \boldsymbol{\beta}_1=\left(\begin{array}{l}1 \\0 \\1\end{array}\right)-\frac{(-1)}{2}\left(\begin{array}{c}-1 \\1 \\0\end{array}\right)=\frac{1}{2}\left(\begin{array}{l}1 \\1 \\2\end{array}\right), \end{aligned} β 2 = ξ 2 − ∥ β 1 ∥ 2 ( β 1 , ξ 2 ) β 1 = 1 0 1 − 2 ( − 1 ) − 1 1 0 = 2 1 1 1 2 , β 3 = ξ 3 = ( − 1 − 1 1 ) \displaystyle \begin{aligned} \boldsymbol{\beta}_3=\boldsymbol{\xi}_3=\left(\begin{array}{c}-1 \\-1 \\1\end{array}\right)\end{aligned} β 3 = ξ 3 = − 1 − 1 1 实对称矩阵不同特征值的特征向量相互正交,β 3 \boldsymbol{\beta}_3 β 3 将 β 1 , β 2 , β 3 单位化. \displaystyle \begin{aligned} \text { 将 } \boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3 \text { 单位化. } \end{aligned} 将 β 1 , β 2 , β 3 单位化 . ε 1 = β 1 ∥ β 1 ∥ = 1 2 ( − 1 1 0 ) , \displaystyle \begin{aligned} \boldsymbol{\varepsilon}_1=\frac{\boldsymbol{\beta}_1}{\left\|\boldsymbol{\beta}_1\right\|}=\frac{1}{\sqrt{2}}\left(\begin{array}{c}-1 \\1 \\0\end{array}\right), \end{aligned} ε 1 = ∥ β 1 ∥ β 1 = 2 1 − 1 1 0 , ε 2 = β 2 ∥ β 2 ∥ = 1 6 ( 1 1 2 ) \displaystyle \begin{aligned}\boldsymbol{\varepsilon}_2=\frac{\boldsymbol{\beta}_2}{\left\|\boldsymbol{\beta}_2\right\|}=\frac{1}{\sqrt{6}}\left(\begin{array}{c}1 \\1 \\2\end{array}\right)\end{aligned} ε 2 = ∥ β 2 ∥ β 2 = 6 1 1 1 2 ε 3 = β 3 ∥ β 3 ∥ = 1 3 ( − 1 − 1 1 ) . \displaystyle \begin{aligned}\boldsymbol{\varepsilon}_3=\frac{\boldsymbol{\beta}_3}{\left\|\boldsymbol{\beta}_3\right\|}=\frac{1}{\sqrt{3}}\left(\begin{array}{c}-1 \\-1 \\1\end{array}\right) .\end{aligned} ε 3 = ∥ β 3 ∥ β 3 = 3 1 − 1 − 1 1 . 存在正交矩阵 P ,使得\displaystyle \begin{aligned}P^T A P = \Lambda = \left(\begin{array} a-1 & & \\ & a-1 \\ & & a+2 \end{array}\right)\end{aligned} C 2 = ( a + 3 ) E − A \boldsymbol{C}^{2}=(a+3) \boldsymbol{E}-\boldsymbol{A} C 2 = ( a + 3 ) E − A ( a + 3 ) E − A = ( 3 − 1 1 − 1 3 1 1 1 3 ) \displaystyle (a+3) E-A=\left(\begin{array}{ccc}3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 3\end{array}\right) ( a + 3 ) E − A = 3 − 1 1 − 1 3 1 1 1 3 C = Q Λ 1 k Q ⊤ , A = C k \displaystyle \begin{aligned} C = Q \Lambda^{\frac{1}{k}} Q^{\top}\text{,} A = C^k \end{aligned} C = Q Λ k 1 Q ⊤ , A = C k 下面就是要把施密特正交公式背下来∶施密特正交化的步骤 β1就是α1∶β 1 = α 1 \beta_1=\alpha_1 β 1 = α 1 β2就是α2减β1∶β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 \beta_2=\alpha_2-\frac{\left(\alpha_2, \beta_1\right)}{\left(\beta_1, \beta_1\right)} \beta_1 β 2 = α 2 − ( β 1 , β 1 ) ( α 2 , β 1 ) β 1 求β2的系数 分子是α2和β1做内积 分母就是β1向量的坐标平方和 β3就是α3减β1再减β2∶β 3 = α 3 − ( α 3 , β 1 ) ( β 1 , β 1 ) β 1 − ( α 3 , β 2 ) ( β 2 , β 2 ) β 2 \beta_3=\alpha_3-\frac{\left(\alpha_3, \beta_1\right)}{\left(\beta_1, \beta_1\right)} \beta_1-\frac{\left(\alpha_3, \beta_2\right)}{\left(\beta_2, \beta_2\right)} \beta_2 β 3 = α 3 − ( β 1 , β 1 ) ( α 3 , β 1 ) β 1 − ( β 2 , β 2 ) ( α 3 , β 2 ) β 2 求β3的系数 β1的系数∶分子是α3和β1的内积,分母仍然是β1的坐标平方和 这样得到的三个向量肯定两两垂直, 这三个系数起什么作用?要保证这三个向量一定是两两垂直的 下一步单位化 γ 1 = β 1 ∥ β 1 ∥ γ 2 = β 2 ∥ β 2 ∥ γ 3 = β 3 ∥ β 3 ∥ \displaystyle \gamma_1=\frac{\beta_1}{\left\|\beta_1\right\|} \quad \gamma_2=\frac{\beta_2}{\left\|\beta_2\right\|} \quad \gamma_3=\frac{\beta_3}{\left\|\beta_3\right\|} γ 1 = ∥ β 1 ∥ β 1 γ 2 = ∥ β 2 ∥ β 2 γ 3 = ∥ β 3 ∥ β 3 γ i = β i ∥ β i ∥ ( i = 1 , 2 , 3 ) \gamma_i=\frac{\beta_i}{\left\|\beta_i\right\|}(i=1,2,3) γ i = ∥ β i ∥ β i ( i = 1 , 2 , 3 ) 单位化后,得到的就是将两两垂直的向量,变成长度是1的单位向量 若 n \displaystyle \begin{aligned} n \end{aligned} n A \displaystyle \begin{aligned} A \end{aligned} A λ 1 , λ 2 , ⋯ , λ n \displaystyle \begin{aligned} \lambda_1, \lambda_2, \cdots, \lambda_n \end{aligned} λ 1 , λ 2 , ⋯ , λ n C \displaystyle \begin{aligned} C \end{aligned} C A = C k \displaystyle \begin{aligned} A = C^k \end{aligned} A = C k ∃ P \displaystyle \exists P ∃ P P − 1 A P = Λ → A = P Λ P − 1 = P ( Λ 1 k ⋅ Λ 1 k ⋯ Λ 1 k ) P − 1 P^{-1} A P = \Lambda \rightarrow A = P \Lambda P^{-1} = P \left( \Lambda^{\frac{1}{k}} \cdot \Lambda^{\frac{1}{k}} \cdots \Lambda^{\frac{1}{k}} \right) P^{-1} P − 1 A P = Λ → A = P Λ P − 1 = P ( Λ k 1 ⋅ Λ k 1 ⋯ Λ k 1 ) P − 1 = P Λ 1 k P − 1 ⋅ P Λ 1 k P − 1 ⋯ ⋅ P Λ 1 k P − 1 \displaystyle \begin{aligned} = P \Lambda^{\frac{1}{k}} P^{-1} \cdot P \Lambda^{\frac{1}{k}} P^{-1} \cdots \cdot P \Lambda^{\frac{1}{k}} P^{-1} \end{aligned} = P Λ k 1 P − 1 ⋅ P Λ k 1 P − 1 ⋯ ⋅ P Λ k 1 P − 1 ∴ C = P Λ 1 k P − 1 ⋅ A = C k \displaystyle \begin{aligned} \therefore C = P \Lambda^{\frac{1}{k}} P^{-1} \cdot A = C^k \end{aligned} ∴ C = P Λ k 1 P − 1 ⋅ A = C k ∃ Q \displaystyle \exists Q ∃ Q Q ⊤ A Q = Λ . → A = Q Λ Q ⊤ = Q ( Λ 1 k ) Q ⊤ Q^{\top} A Q = \Lambda. \rightarrow A = Q \Lambda Q^{\top} = Q \left( \Lambda^{\frac{1}{k}} \right) Q^{\top} Q ⊤ A Q = Λ. → A = Q Λ Q ⊤ = Q ( Λ k 1 ) Q ⊤ = Q Λ 1 k Q ⊤ ⋯ ⋅ Q Λ 1 k Q ⊤ \displaystyle \begin{aligned} = Q \Lambda^{\frac{1}{k}} Q^{\top} \cdots \cdot Q \Lambda^{\frac{1}{k}} Q^{\top} \end{aligned} = Q Λ k 1 Q ⊤ ⋯ ⋅ Q Λ k 1 Q ⊤ C = Q Λ 1 k Q ⊤ , A = C k \displaystyle \begin{aligned} C = Q \Lambda^{\frac{1}{k}} Q^{\top}\text{,} A = C^k \end{aligned} C = Q Λ k 1 Q ⊤ , A = C k (22) (本题满分 12 分)( 0 , 2 ) (0,2) ( 0 , 2 ) X X X Y Y Y Z = Y X Z=\frac{Y}{X} Z = X Y X X X Z Z Z E ( X Y ) E\left(\frac{X}{Y}\right) E ( Y X )
(22) 解X X X 定义 X X X X = min { V , 2 − V } X = \min\{V, 2-V\} X = min { V , 2 − V } 如果超过1,就成了较长的一段,而不是较短的一段 x为长度,而不是(0,2)上的区间 若随机变量 X ∼ U ( a , b ) X \sim U(a, b) X ∼ U ( a , b ) X X X f ( x ) = { 1 b − a , a < x < b 0 , 其他. \displaystyle f(x)=\left\{\begin{array}{ll}\frac{1}{b-a}, & a<x<b \\0, & \text { 其他. }\end{array}\right. f ( x ) = { b − a 1 , 0 , a < x < b 其他 . x ∼ ∪ ( 0 , 1 ) x \sim \cup(0,1) x ∼ ∪ ( 0 , 1 ) 概率密度=区间长度分之一∴ f x ( x ) = { 1 , 0 < x < 1 0 else \displaystyle \therefore f_x(x)=\left\{\begin{array}{lc}1 , & 0<x<1 \\ 0 & \text { else }\end{array}\right. ∴ f x ( x ) = { 1 , 0 0 < x < 1 else Z Z Z 定义 Z Z Z Z = Y X = X + Y = 2 2 − X X = 2 X − 1 Z = \frac{Y}{X} \xlongequal[]{X+Y=2} \frac{2-X}{X}=\frac{2}{X}-1 Z = X Y X + Y = 2 X 2 − X = X 2 − 1 如何讨论 如果x是离散型,则不用画进图中,直接用全集分解来分类讨论 只有连续型的范围,才画入图中 如果X和Y都是离散型,如何画图 如果X和Y都是连续型,如何画图 x,y,z都存在,则画出(x,y)的区间,然后让z=f(x,y)在这个区间从下往上刷 如果X和Y一个离散,一个连续,如何画图 只剩(x和z)或(y和z) 将x=g(z)反函数之后,就是从左往右刷 没有用反函数,还是z=f(x)的时候,就从下往上刷 由x的范围,y的范围和函数Z=g(X,Y)三者围成的区间画图z = 2 x − 1 z = \frac{2}{x}-1 z = x 2 − 1 x = 2 z + 1 x = \frac{2}{z+1} x = z + 1 2 然后直接三件套z < 1 z<1 z < 1 → 写出分布函数 F Z ( z ) = 定义 P { Z ⩽ z } = 转化 0 \xrightarrow[]{\text{写出分布函数}}F_Z(z)\xlongequal[]{\text{定义}}P\{Z \leqslant z\}\xlongequal[]{\text{转化}}0 写出分布函数 F Z ( z ) 定义 P { Z ⩽ z } 转化 0 z ⩾ 1 z \geqslant 1 z ⩾ 1 → 写出分布函数 F Z ( z ) = 定义 P { Z ⩽ z } = Z = 2 X − 1 转化 P { 2 X − 1 ⩽ z } = 反函数 P { X ⩾ 2 z + 1 } \xrightarrow[]{\text{写出分布函数}}F_Z(z)\xlongequal[]{\text{定义}}P\{Z \leqslant z\}\xlongequal[Z=\frac{2}{X}-1]{\text{转化}}P\left\{\frac{2}{X}-1 \leqslant z\right\}\xlongequal[]{\text{反函数}}P\left\{X \geqslant \frac{2}{z+1}\right\} 写出分布函数 F Z ( z ) 定义 P { Z ⩽ z } 转化 Z = X 2 − 1 P { X 2 − 1 ⩽ z } 反函数 P { X ⩾ z + 1 2 } = 根据 x 的积分上下限 ∫ 2 z + 1 1 1 d x = 1 − 2 z + 1 . \displaystyle \xlongequal[]{\text{根据}x\text{的积分上下限}}\int_{\frac{2}{z+1}}^1 1 \mathrm{~d} x=1-\frac{2}{z+1} . 根据 x 的积分上下限 ∫ z + 1 2 1 1 d x = 1 − z + 1 2 . Z Z Z 利用 X X X Z Z Z X X X f Z ( z ) = { 2 ( 1 + z ) 2 , z > 1 , 0 , 其他 . \displaystyle f_Z(z) = \begin{cases}\frac{2}{(1+z)^2}, & z > 1, \\ 0, & \text{其他}.\end{cases} f Z ( z ) = { ( 1 + z ) 2 2 , 0 , z > 1 , 其他 . E ( X Y ) E\left(\frac{X}{Y}\right) E ( Y X ) 计算期望值:求谁的期望,在谁前面乘概率密度进行积分 E ( X Y ) = E ( X 2 − X ) = ∫ − ∞ + ∞ x 2 − x ⋅ f X ( x ) d x = 何处求积分 f X ( x ) = 1 ∫ 0 1 x 2 − x d x = 2 ln 2 − 1 \displaystyle E\left(\frac{X}{Y}\right) =E\left(\frac{X}{2-X}\right) =\int_{-\infty}^{+\infty} \frac{x}{2-x} \cdot f_X(x) \mathrm{d} x\xlongequal[\text{何处求积分}]{f_X(x) =1}\int_0^1 \frac{x}{2-x} dx=2 \ln 2 - 1 E ( Y X ) = E ( 2 − X X ) = ∫ − ∞ + ∞ 2 − x x ⋅ f X ( x ) d x f X ( x ) = 1 何处求积分 ∫ 0 1 2 − x x d x = 2 ln 2 − 1 小崔版 (1) 令点为 M . M ∼ U ( 0.2 ) \displaystyle \begin{aligned} &\text { (1) 令点为 } M . M \sim U(0.2) \end{aligned} (1) 令点为 M . M ∼ U ( 0.2 ) f M ( m ) = { 1 2 0 < m < 2 0 其 0 . F M ( m ) = { 0 m < 0 m 2 0 ⩽ m < 2 1 2 ⩽ m \displaystyle \begin{aligned} f_M(m)=\left\{\begin{array}{cc}\frac{1}{2} & 0<m<2 \\0 & \text { 其 } 0\end{array} . \quad F_M(m)=\left\{\begin{array}{cc}0 & m<0 \\\frac{m}{2} & 0 \leqslant m<2 \\1 & 2 \leqslant m\end{array}\right.\right. \end{aligned} f M ( m ) = ⎩ ⎨ ⎧ 2 1 0 0 < m < 2 其 0 . F M ( m ) = ⎩ ⎨ ⎧ 0 2 m 1 m < 0 0 ⩽ m < 2 2 ⩽ m X = min { M , 2 − M } \displaystyle \begin{aligned} X=\min \{M, 2-M\} \end{aligned} X = min { M , 2 − M } F x ( x ) = P { X ⩽ x } = P { min { M , 2 − M } ⩽ x } \displaystyle \begin{aligned} F_x(x) & =P\{X \leqslant x\}=P\{\min \{M, 2-M\} \leqslant x\} \end{aligned} F x ( x ) = P { X ⩽ x } = P { min { M , 2 − M } ⩽ x } = 1 − P { min { M , 2 − M } > x } = 1 − P { M > x .2 − M > x } \displaystyle \begin{aligned} =1-P\{\min \{M, 2-M\}>x\}=1-P\{M>x .2-M>x\} \end{aligned} = 1 − P { min { M , 2 − M } > x } = 1 − P { M > x .2 − M > x } = 1 − P { M > x , M < 2 − x } \displaystyle \begin{aligned} =1-P\{M>x \text{,}M<2-x\} \end{aligned} = 1 − P { M > x , M < 2 − x } { 1 ∘ 若 x < 0 时. F x ( x ) = 0. 2 ∘ 若 0 ⩽ x < 1 时. F x ( x ) = 1 − P { x < M < 2 − x } = 1 − ∫ x 2 − x 1 2 d m = x 3 ∘ 若 1 ⩽ x 时. F x ( x ) = 1 . $ . \displaystyle \begin{aligned} & \left\{\begin{array}{l}1^{\circ} \text { 若 } x<0 \text { 时. } F_x(x)=0 . \\2^{\circ} \text { 若 } 0 \leqslant x<1 \text { 时. } F_x(x)=1-P\{x<M<2-x\}=1-\int_x^{2-x} \frac{1}{2} d m=x \\3^{\circ} \text { 若 } 1 \leqslant x \text { 时. } F_x(x)=1 \end{array} . \$ .\right. \end{aligned} ⎩ ⎨ ⎧ 1 ∘ 若 x < 0 时 . F x ( x ) = 0. 2 ∘ 若 0 ⩽ x < 1 时 . F x ( x ) = 1 − P { x < M < 2 − x } = 1 − ∫ x 2 − x 2 1 d m = x 3 ∘ 若 1 ⩽ x 时 . F x ( x ) = 1 .$. ⇒ f x ( x ) = { 1 0 < x < 1 0 其他 \displaystyle \begin{aligned}\Rightarrow f_x(x)= \begin{cases}1 & 0<x<1 \\0 & \text { 其他 }\end{cases}\end{aligned} ⇒ f x ( x ) = { 1 0 0 < x < 1 其他 F 2 ( z ) = P { Z ⩽ z } = P { 2 − X X ⩽ z } = P { 2 X − 1 ⩽ z } \displaystyle F_2(z) =P\{Z\leqslant z\}=P\left\{\frac{2-X}{X} \leqslant z\right\}=P\left\{\frac{2}{X}-1 \leqslant z\right\} F 2 ( z ) = P { Z ⩽ z } = P { X 2 − X ⩽ z } = P { X 2 − 1 ⩽ z } = P { x ⩾ 2 z + 1 } \displaystyle =P\left\{x \geqslant \frac{2}{z+1}\right\} = P { x ⩾ z + 1 2 } z < 1 z<1 z < 1 F 2 ( z ) = 0 F_2(z)=0 F 2 ( z ) = 0 1 ⩽ z 1 \leqslant z 1 ⩽ z F 2 ( z ) = P { x ⩾ 2 z + 1 } = x 密度为 1 x ∈ ( 0 , 1 ) ∫ 2 z + 1 1 1 d x = 1 − 2 3 + 1 F_2(z)=P\left\{x \geqslant \frac{2}{z+1}\right\}\xlongequal[x\text{密度为}1]{x\in(0,1)} \int_{\frac{2}{z+1}}^1 1 d x=1-\frac{2}{3+1} F 2 ( z ) = P { x ⩾ z + 1 2 } x ∈ ( 0 , 1 ) x 密度为 1 ∫ z + 1 2 1 1 d x = 1 − 3 + 1 2 E ( X Y ) = E ( X 2 − X ) = ∫ − ∞ + ∞ x 2 − x ⋅ f x ( x ) d x \displaystyle E\left(\frac{X}{Y}\right) =E\left(\frac{X}{2-X}\right)=\int_{-\infty}^{+\infty} \frac{x}{2-x} \cdot f_x(x) d x E ( Y X ) = E ( 2 − X X ) = ∫ − ∞ + ∞ 2 − x x ⋅ f x ( x ) d x = f X ( x ) = 1 ∫ 0 1 x 2 − x d x = − 2 + 2 ∫ 0 1 − 1 + 2 2 − x d x \displaystyle \xlongequal[]{f_X(x) =1}\int_0^1 \frac{x}{2-x} d x\xlongequal[]{-2+2}\int_0^1-1+\frac{2}{2-x} d x f X ( x ) = 1 ∫ 0 1 2 − x x d x − 2 + 2 ∫ 0 1 − 1 + 2 − x 2 d x = − x − 2 ln ∣ 2 − x ∣ ∣ 0 1 = 2 ln 2 − 1 \displaystyle =-x-\left.2 \ln |2-x|\right|_0 ^1=2 \ln 2-1 = − x − 2 ln ∣2 − x ∣ ∣ 0 1 = 2 ln 2 − 1