一、选择题 (本题共 8 小题, 每小题 4 分, 共 32 分. 在每小题给出的四个选项中, 只有一项符合题目 要求,把所选项前的字母填在题后的括号内. )
(1) 若函数 f ( x ) = { 1 − cos x a x , x > 0 , b , x ⩽ 0 \displaystyle f(x)=\left\{\begin{array}{ll}\frac{1-\cos \sqrt{x}}{a x}, & x>0, \\ b, & x \leqslant 0\end{array}\right. f ( x ) = { a x 1 − c o s x , b , x > 0 , x ⩽ 0 x = 0 x=0 x = 0 ( ) (\quad) ( ) a b = 1 2 a b=\frac{1}{2} ab = 2 1 a b = − 1 2 a b=-\frac{1}{2} ab = − 2 1 a b = 0 a b=0 ab = 0 a b = 2 a b=2 ab = 2
(1) 要使函数在 x = 0 x=0 x = 0 f ( x ) f(x) f ( x ) 计算右极限 lim x → 0 + 1 − cos x a x = 1 − ( x ) 2 2 lim x → 0 + 1 2 x a x = 1 2 a \displaystyle \lim_{x \rightarrow 0^+} \frac{1-\cos \sqrt{x}}{ax}\xlongequal[]{1 - \frac{(\sqrt{x})^2}{2}}\lim_{x \rightarrow 0^+} \frac{\frac{1}{2}x}{ax} = \frac{1}{2a} x → 0 + lim a x 1 − cos x 1 − 2 ( x ) 2 x → 0 + lim a x 2 1 x = 2 a 1 计算左极限:lim x → 0 − b = b \displaystyle \lim_{x \rightarrow 0^-} b = b x → 0 − lim b = b 左极限=右极限=函数值:1 2 a = b \frac{1}{2a} = b 2 a 1 = b (2) 设函数 f ( x ) f(x) f ( x ) f ( x ) f ′ ( x ) > 0 f(x) f^{\prime}(x)>0 f ( x ) f ′ ( x ) > 0 ( ) (\quad) ( ) f ( 1 ) > f ( − 1 ) f(1)>f(-1) f ( 1 ) > f ( − 1 ) f ( 1 ) < f ( − 1 ) f(1)<f(-1) f ( 1 ) < f ( − 1 ) ∣ f ( 1 ) ∣ > ∣ f ( − 1 ) ∣ |f(1)|>|f(-1)| ∣ f ( 1 ) ∣ > ∣ f ( − 1 ) ∣ ∣ f ( 1 ) ∣ < ∣ f ( − 1 ) ∣ |f(1)|<|f(-1)| ∣ f ( 1 ) ∣ < ∣ f ( − 1 ) ∣
(2) 判断 f ( x ) f ′ ( x ) > 0 f(x) f'(x) > 0 f ( x ) f ′ ( x ) > 0 f ( x ) f(x) f ( x ) 构造辅助函数 g ( x ) = 1 2 f 2 ( x ) g(x) = \frac{1}{2} f^2(x) g ( x ) = 2 1 f 2 ( x ) g ( x ) g(x) g ( x ) 分析 g ( x ) g(x) g ( x ) 由 g ′ ( x ) = f ( x ) f ′ ( x ) > 0 g'(x) = f(x) f'(x) > 0 g ′ ( x ) = f ( x ) f ′ ( x ) > 0 g ( x ) g(x) g ( x ) 比较 g ( 1 ) g(1) g ( 1 ) g ( − 1 ) g(-1) g ( − 1 ) 由1 > − 1 1>-1 1 > − 1 → g ′ ( x ) > 0 g ( 1 ) > g ( − 1 ) \displaystyle \xrightarrow[]{g^{\prime}(x)>0} g(1) > g(-1) g ′ ( x ) > 0 g ( 1 ) > g ( − 1 ) → g ( x ) = 1 2 f 2 ( x ) 1 2 f 2 ( 1 ) > 1 2 f 2 ( − 1 ) \displaystyle \xrightarrow[]{g(x) = \frac{1}{2} f^2(x)}\frac{1}{2} f^2(1) > \frac{1}{2} f^2(-1) g ( x ) = 2 1 f 2 ( x ) 2 1 f 2 ( 1 ) > 2 1 f 2 ( − 1 ) 进一步得到 f 2 ( 1 ) > f 2 ( − 1 ) → 开根号 ∣ f ( 1 ) ∣ > ∣ f ( − 1 ) ∣ f^2(1) > f^2(-1)\xrightarrow[]{\text{开根号}}|f(1)| > |f(-1)| f 2 ( 1 ) > f 2 ( − 1 ) 开根号 ∣ f ( 1 ) ∣ > ∣ f ( − 1 ) ∣ (3) 函数 f ( x , y , z ) = x 2 y + z 2 f(x, y, z)=x^{2} y+z^{2} f ( x , y , z ) = x 2 y + z 2 ( 1 , 2 , 0 ) (1,2,0) ( 1 , 2 , 0 ) n = ( 1 , 2 , 2 ) \boldsymbol{n}=(1,2,2) n = ( 1 , 2 , 2 ) ( ) (\quad) ( )
(3) 答 应选(D).
设函数 f ( x , y , z ) f(x, y, z) f ( x , y , z ) ( x 0 , y 0 , z 0 ) \left(x_0, y_0, z_0\right) ( x 0 , y 0 , z 0 ) e l = ( cos α , cos β , cos γ ) \boldsymbol{e}_l=(\cos \alpha, \cos \beta, \cos \gamma) e l = ( cos α , cos β , cos γ ) l l l f ( x , y , z ) f(x, y, z) f ( x , y , z ) ( x 0 , y 0 , z 0 ) \left(x_0, y_0, z_0\right) ( x 0 , y 0 , z 0 ) l l l ∂ f ∂ l ∣ ( x 0 , y 0 , z 0 ) = grad f ( x 0 , y 0 , z 0 ) ⋅ e l = ∂ f ∂ x ∣ ( x 0 , y 0 , z 0 ) cos α + ∂ f ∂ y ∣ ( x 0 , y 0 , z 0 ) cos β + ∂ f ∂ z ∣ ( x 0 , y 0 , z 0 ) cos γ . \left.\frac{\partial f}{\partial \boldsymbol{l}}\right|_{\left(x_0, y_0, z_0\right)}=\operatorname{grad} f\left(x_0, y_0, z_0\right) \cdot \boldsymbol{e}_l=\left.\frac{\partial f}{\partial x}\right|_{\left(x_0, y_0, z_0\right)} \cos \alpha+\left.\frac{\partial f}{\partial y}\right|_{\left(x_0, y_0, z_0\right)} \cos \beta+\left.\frac{\partial f}{\partial z}\right|_{\left(x_0, y_0, z_0\right)} \cos \gamma . ∂ l ∂ f ( x 0 , y 0 , z 0 ) = grad f ( x 0 , y 0 , z 0 ) ⋅ e l = ∂ x ∂ f ( x 0 , y 0 , z 0 ) cos α + ∂ y ∂ f ( x 0 , y 0 , z 0 ) cos β + ∂ z ∂ f ( x 0 , y 0 , z 0 ) cos γ . n ∥ n ∥ = cos α , cos β , cos γ = ( 1 3 , 2 3 , 2 3 ) \displaystyle \frac{n}{\|n\|}=\cos \alpha, \cos \beta,\cos \gamma=\left(\frac{1}{3}, \frac{2}{3}, \frac{2}{3}\right) ∥ n ∥ n = cos α , cos β , cos γ = ( 3 1 , 3 2 , 3 2 ) ∂ f ∂ n ⃗ = ( f x , f y , f z ) ⋅ ( cos α , cos β , cos γ ‾ ) \displaystyle \frac{\partial f}{\partial \vec{n}} \left.=\left(f_x, f_y, f_z\right) \cdot \underline{(\cos \alpha, \cos \beta,\cos \gamma}\right) ∂ n ∂ f = ( f x , f y , f z ) ⋅ ( cos α , cos β , cos γ ) = ( 2 x y , x 2 , 2 z ) ⋅ ( 1 3 , 2 3 , 2 3 ) \displaystyle =\left(2 x y, x^2, 2 z\right) \cdot\left(\frac{1}{3},\frac{2}{3}, \frac{2}{3}\right) = ( 2 x y , x 2 , 2 z ) ⋅ ( 3 1 , 3 2 , 3 2 ) = ( 4 , 1 , 0 ) ⋅ ( 1 3 , 2 3 , 2 3 ) \displaystyle =(4,1,0) \cdot\left(\frac{1}{3}, \frac{2}{3}, \frac{2}{3}\right) = ( 4 , 1 , 0 ) ⋅ ( 3 1 , 3 2 , 3 2 ) = 4 3 + 2 3 = 2 \displaystyle =\frac{4}{3}+\frac{2}{3}=2 = 3 4 + 3 2 = 2 (4) 甲、乙两人赛跑, 计时开始时, 甲在乙前方 10 (单位: m m m v = v 1 ( t ) v=v_{1}(t) v = v 1 ( t ) m / s ) \left.\mathrm{m} / \mathrm{s}\right) m / s ) v = v 2 ( t ) v=v_{2}(t) v = v 2 ( t ) 10 , 20 , 3 10,20,3 10 , 20 , 3 t 0 t_{0} t 0 s \mathrm{s} s ( ) (\quad) ( ) t 0 = 10 t_{0}=10 t 0 = 10 15 < t 0 < 20 15<t_{0}<20 15 < t 0 < 20 t 0 = 25 t_{0}=25 t 0 = 25 t 0 > 25 t_{0}>25 t 0 > 25
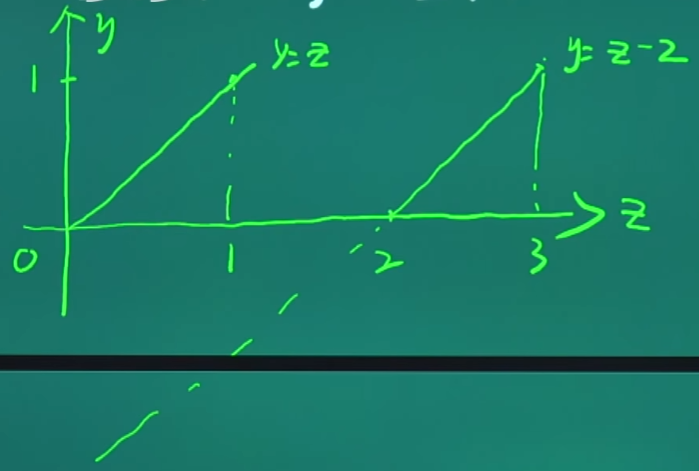
(4) 答 应选(C).t 0 t_0 t 0 S 1 = ∫ 0 t 0 v 1 ( t ) d t , S 2 = ∫ 0 t 0 v 2 ( t ) d t , \displaystyle S_1=\int_0^{t_0} v_1(t) \mathrm{d} t, S_2=\int_0^{t_0} v_2(t) \mathrm{d} t, S 1 = ∫ 0 t 0 v 1 ( t ) d t , S 2 = ∫ 0 t 0 v 2 ( t ) d t , S 1 S_1 S 1 v = v 1 ( t ) , t = t 0 v=v_1(t), t=t_0 v = v 1 ( t ) , t = t 0 S 2 S_2 S 2 v = v 2 ( t ) , t = v=v_2(t), t= v = v 2 ( t ) , t = t 0 t_0 t 0 t 0 t_0 t 0 S 2 = S 1 + 10 , S_2=S_1+10 \text {, } S 2 = S 1 + 10 , ∫ 0 t 0 v 2 ( t ) d t = ∫ 0 t 0 v 1 ( t ) d t + 10 , \displaystyle \int_0^{t_0} v_2(t) \mathrm{d} t=\int_0^{t_0} v_1(t) \mathrm{d} t+10, ∫ 0 t 0 v 2 ( t ) d t = ∫ 0 t 0 v 1 ( t ) d t + 10 , ∫ 0 t 0 [ v 2 ( t ) − v 1 ( t ) ] d t = 10. \displaystyle \int_0^{t_0}\left[v_2(t)-v_1(t)\right] \mathrm{d} t=10 . ∫ 0 t 0 [ v 2 ( t ) − v 1 ( t ) ] d t = 10. t 0 = 25 t_0=25 t 0 = 25 (5) 设 α \boldsymbol{\alpha} α n n n E \boldsymbol{E} E n n n ( ) (\quad) ( ) E − α α T \boldsymbol{E}-\boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} E − α α T E + α α T \boldsymbol{E}+\boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} E + α α T E + 2 α α T \boldsymbol{E}+2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} E + 2 α α T E − 2 α α T \boldsymbol{E}-2 \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} E − 2 α α T
(5) 答 应选 ( A ) (A) ( A ) A \boldsymbol{A} A A \boldsymbol{A} A α α T \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} α α T α \boldsymbol{\alpha} α α T α = 1 \boldsymbol{\alpha}^{\mathrm{T}} \boldsymbol{\alpha}=1 α T α = 1 α α T \boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} α α T n − 1 n-1 n − 1 E − α α T \boldsymbol{E}-\boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} E − α α T n − 1 n-1 n − 1 E − α α T \boldsymbol{E}-\boldsymbol{\alpha} \boldsymbol{\alpha}^{\mathrm{T}} E − α α T (6) 已知矩阵 A = ( 2 0 0 0 2 1 0 0 1 ) , B = ( 2 1 0 0 2 0 0 0 1 ) , C = ( 1 0 0 0 2 0 0 0 2 ) \displaystyle \boldsymbol{A}=\left(\begin{array}{lll}2 & 0 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 1\end{array}\right), \boldsymbol{B}=\left(\begin{array}{lll}2 & 1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1\end{array}\right), \boldsymbol{C}=\left(\begin{array}{lll}1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2\end{array}\right) A = 2 0 0 0 2 0 0 1 1 , B = 2 0 0 1 2 0 0 0 1 , C = 1 0 0 0 2 0 0 0 2 A \boldsymbol{A} A C \boldsymbol{C} C B \boldsymbol{B} B C \boldsymbol{C} C A \boldsymbol{A} A C \boldsymbol{C} C B \boldsymbol{B} B C \boldsymbol{C} C A \boldsymbol{A} A C \boldsymbol{C} C B \boldsymbol{B} B C \boldsymbol{C} C A \boldsymbol{A} A C \boldsymbol{C} C B \boldsymbol{B} B C \boldsymbol{C} C
(6) 答 应选(B). A \boldsymbol{A} A B \boldsymbol{B} B 2 , 2 , 1 2,2,1 2 , 2 , 1 问相似 先看特征值:ABC的是全相等的 再看是否有二重根 如果有二重根,看有几个线性无关的解 :用∣ A − λ E ∣ |A-\lambda E| ∣ A − λ E ∣ B选项,是二重根,但只有一个线性无关的特征向量,因此不能相似对角化 它们是否与 C \boldsymbol{C} C 矩阵 A \boldsymbol{A} A 2 , n − r ( 2 E − A ) = 3 − 1 = 2 2, n-r(2 \boldsymbol{E}-\boldsymbol{A})=3-1=2 2 , n − r ( 2 E − A ) = 3 − 1 = 2 2 E − A = ( 0 0 0 0 0 − 1 0 0 1 ) \displaystyle 2 \boldsymbol{E}-\boldsymbol{A}=\left(\begin{array}{ccc}0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 0 & 1\end{array}\right) 2 E − A = 0 0 0 0 0 0 0 − 1 1 于是 A \boldsymbol{A} A A \boldsymbol{A} A C \boldsymbol{C} C 矩阵 B \boldsymbol{B} B 2 , n − r ( 2 E − B ) = 3 − 2 = 1 2, n-r(2 \boldsymbol{E}-\boldsymbol{B})=3-2=1 2 , n − r ( 2 E − B ) = 3 − 2 = 1 2 E − B = ( 0 − 1 0 0 0 0 0 0 1 ) \displaystyle 2 \boldsymbol{E}-\boldsymbol{B}=\left(\begin{array}{ccc}0 & -1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1\end{array}\right) 2 E − B = 0 0 0 − 1 0 0 0 0 1 于是 B \boldsymbol{B} B B \boldsymbol{B} B C \boldsymbol{C} C (7) 设 A , B A, B A , B 0 < P ( A ) < 1 , 0 < P ( B ) < 1 0<P(A)<1,0<P(B)<1 0 < P ( A ) < 1 , 0 < P ( B ) < 1 P ( A ∣ B ) > P ( A ∣ B ˉ ) ⏟ 用条件概率公式展开 \underbrace{P(A \mid B)>P(A \mid \bar{B})}_{\text{用条件概率公式展开}} 用条件概率公式展开 P ( A ∣ B ) > P ( A ∣ B ˉ ) ( ) (\quad) ( ) P ( B ∣ A ) > P ( B ∣ A ˉ ) ⏟ 用条件概率公式展开 \underbrace{P(B \mid A)>P(B \mid \bar{A})}_{\text{用条件概率公式展开}} 用条件概率公式展开 P ( B ∣ A ) > P ( B ∣ A ˉ ) P ( B ∣ A ) < P ( B ∣ A ˉ ) P(B \mid A)<P(B \mid \bar{A}) P ( B ∣ A ) < P ( B ∣ A ˉ ) P ( B ˉ ∣ A ) > P ( B ∣ A ˉ ) P(\bar{B} \mid A)>P(B \mid \bar{A}) P ( B ˉ ∣ A ) > P ( B ∣ A ˉ ) P ( B ˉ ∣ A ) < P ( B ∣ A ˉ ) P(\bar{B} \mid A)<P(B \mid \bar{A}) P ( B ˉ ∣ A ) < P ( B ∣ A ˉ )
(7) 解 应选 (A).
题设条件 P ( A ∣ B ) > P ( A ∣ B ˉ ) → 两边条件概率 P ( A B ) P ( B ) > P ( A B ˉ ) P ( B ˉ ) = 求逆 P ( A ) − P ( A B ) 1 − P ( B ) , P(A \mid B)>P(A \mid \bar{B})\xrightarrow[]{\text{两边条件概率}}\frac{P(A B)}{P(B)}>\frac{P(A \bar{B})}{P(\bar{B})}\xlongequal[]{\text{求逆}}\frac{P(A)-P(A B)}{1-P(B)}, P ( A ∣ B ) > P ( A ∣ B ˉ ) 两边条件概率 P ( B ) P ( A B ) > P ( B ˉ ) P ( A B ˉ ) 求逆 1 − P ( B ) P ( A ) − P ( A B ) , 则P ( A B ) P ( B ) > P ( A ) − P ( A B ) 1 − P ( B ) \displaystyle \frac{P(A B)}{P(B)}>\frac{P(A)-P(A B)}{1-P(B)} P ( B ) P ( A B ) > 1 − P ( B ) P ( A ) − P ( A B ) P ( A B ) [ 1 − P ( B ) ] > P ( B ) [ P ( A ) − P ( A B ) ] P(A B)[1-P(B)]>P(B)[P(A)-P(A B)] P ( A B ) [ 1 − P ( B )] > P ( B ) [ P ( A ) − P ( A B )] → P ( B ) P ( A B ) 左右两边消去 P ( A B ) > P ( A ) P ( B ) \displaystyle \xrightarrow[P(B) P(A B)]{\text{左右两边消去}}P(A B)>P(A) P(B) 左右两边消去 P ( B ) P ( A B ) P ( A B ) > P ( A ) P ( B ) 综上, P ( A ∣ B ) > P ( A ∣ B ˉ ) P(A \mid B)>P(A \mid \bar{B}) P ( A ∣ B ) > P ( A ∣ B ˉ ) P ( A B ) > P ( A ) P ( B ) P(A B)>P(A) P(B) P ( A B ) > P ( A ) P ( B ) 对于A选项:P ( B ∣ A ) > P ( B ∣ A ˉ ) P(B \mid A)>P(B \mid \bar{A}) P ( B ∣ A ) > P ( B ∣ A ˉ ) P ( A B ) P ( A ) > P ( B A ˉ ) P ( A ˉ ) = P ( B ) − P ( A B ) 1 − P ( A ) \displaystyle \frac{P(A B)}{P(A)}>\frac{P(B \bar{A})}{P(\bar{A})} =\frac{P(B)-P(A B)}{1-P(A)} P ( A ) P ( A B ) > P ( A ˉ ) P ( B A ˉ ) = 1 − P ( A ) P ( B ) − P ( A B ) → 不等式交叉相乘 P ( A B ) [ 1 − P ( A ) ] > P ( A ) [ P ( B ) − P ( A B ) ] \displaystyle \xrightarrow[]{\text{不等式交叉相乘}}P(A B)[1-P(A)] >P(A)[P(B)-P(A B)] 不等式交叉相乘 P ( A B ) [ 1 − P ( A )] > P ( A ) [ P ( B ) − P ( A B )] 从而 P ( B A ) > P ( B ) P ( A ) P(B A)>P(B) P(A) P ( B A ) > P ( B ) P ( A ) 则充要条件为 P ( B ∣ A ) > P ( B ∣ A ˉ ) P(B \mid A)>P(B \mid \bar{A}) P ( B ∣ A ) > P ( B ∣ A ˉ ) ( A ) (A) ( A ) (8) 设 X 1 , X 2 , ⋯ , X n ( n ⩾ 2 ) X_{1}, X_{2}, \cdots, X_{n}(n \geqslant 2) X 1 , X 2 , ⋯ , X n ( n ⩾ 2 ) 总体 N ( μ , 1 ) 的简单随机样本 ⏟ n 个正态分布的平方和就是卡方分布 \underbrace{\text{总体} N(\mu, 1) \text{的简单随机样本}}_{n\text{个正态分布的平方和就是卡方分布}} n 个正态分布的平方和就是卡方分布 总体 N ( μ , 1 ) 的简单随机样本 X ˉ = 1 n ∑ i = 1 n X i \displaystyle \bar{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i} X ˉ = n 1 i = 1 ∑ n X i 不正确的 是 ( ) (\quad) ( ) ∑ i = 1 n ( X i − μ ) 2 \displaystyle \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2} i = 1 ∑ n ( X i − μ ) 2 χ 2 \chi^{2} χ 2 2 ( X n − X 1 ) 2 2\left(X_{n}-X_{1}\right)^{2} 2 ( X n − X 1 ) 2 χ 2 \chi^{2} χ 2 ∑ i = 1 n ( X i − X ˉ ) 2 \displaystyle \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} i = 1 ∑ n ( X i − X ˉ ) 2 χ 2 \chi^{2} χ 2 n ( X ˉ − μ ) 2 n(\bar{X}-\mu)^{2} n ( X ˉ − μ ) 2 χ 2 \chi^{2} χ 2
(8) 答 应选(B). 这道题的核心就是要注意卡方分布前面的系数 (A) ∑ i = 1 n ( X i − μ ) 2 \displaystyle \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2} i = 1 ∑ n ( X i − μ ) 2 χ 2 \chi^{2} χ 2 x i − μ ∼ N ( 0 , 1 ) ( x i − μ ) 2 ∼ χ 2 ( 1 ) \displaystyle x_{i} - \mu \sim N(0, 1) \quad (x_{i} - \mu)^{2} \sim \chi^{2}(1) x i − μ ∼ N ( 0 , 1 ) ( x i − μ ) 2 ∼ χ 2 ( 1 ) ∑ i = 1 n ( X i − μ ) 2 = ( X 1 − μ ) 2 + ( X 2 − μ ) 2 + ⋯ + ( X n − μ ) 2 ∼ χ 2 ( n ) \displaystyle \sum_{i=1}^{n} (X_{i} - \mu)^{2} = (X_{1} - \mu)^{2} + (X_{2} - \mu)^{2} + \cdots + (X_{n} - \mu)^{2} \sim \chi^{2}(n) i = 1 ∑ n ( X i − μ ) 2 = ( X 1 − μ ) 2 + ( X 2 − μ ) 2 + ⋯ + ( X n − μ ) 2 ∼ χ 2 ( n ) (B) 2 ( X n − X 1 ) 2 2\left(X_{n}-X_{1}\right)^{2} 2 ( X n − X 1 ) 2 χ 2 \chi^{2} χ 2 X ∼ N ( μ 1 , σ 2 ) Y ∼ N ( μ 2 , σ 2 ) X \displaystyle X \sim N(\mu_1, \sigma^2) \quad Y \sim N(\mu_2, \sigma^2) \quad X X ∼ N ( μ 1 , σ 2 ) Y ∼ N ( μ 2 , σ 2 ) X Y Y Y a X + b Y ∼ N ( a μ 1 + b μ 2 , a 2 σ 1 2 + b 2 σ 2 2 ) \displaystyle aX + bY \sim N(a\mu_1 + b\mu_2, a^2 \sigma_1^2 + b^2 \sigma_2^2) a X + bY ∼ N ( a μ 1 + b μ 2 , a 2 σ 1 2 + b 2 σ 2 2 ) X n − X 1 ∼ N ( 0 , 2 ) X n − X 1 2 ∼ N ( 0 , 1 ) \displaystyle X_n - X_1 \sim N(0, 2) \quad \frac{X_n - X_1}{\sqrt{2}} \sim N(0, 1) X n − X 1 ∼ N ( 0 , 2 ) 2 X n − X 1 ∼ N ( 0 , 1 ) ( X n − X 1 ) 2 2 ∼ χ 2 ( 1 ) \displaystyle \frac{(X_n - X_1)^2}{2} \sim \chi^{2}(1) 2 ( X n − X 1 ) 2 ∼ χ 2 ( 1 ) (C) ∑ i = 1 n ( X i − X ˉ ) 2 \displaystyle \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} i = 1 ∑ n ( X i − X ˉ ) 2 χ 2 \chi^{2} χ 2 ∑ i = 1 n ( X i − X ˉ ) 2 = ( n − 1 ) S 2 1 \displaystyle \sum_{i=1}^n\left(X_i-\bar{X}\right)^2=\frac{(n-1) S^2}{1} i = 1 ∑ n ( X i − X ˉ ) 2 = 1 ( n − 1 ) S 2 由性质(2):( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) → σ = 1 \displaystyle \frac{(n-1) S^2}{\sigma^2} \sim \chi^2(n-1)\xrightarrow[]{\sigma=1 } σ 2 ( n − 1 ) S 2 ∼ χ 2 ( n − 1 ) σ = 1 所以 ∑ i = 1 n ( X i − X ˉ ) 2 ∼ \displaystyle \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 \sim i = 1 ∑ n ( X i − X ˉ ) 2 ∼ χ 2 ( n − 1 ) \chi^2(n-1) χ 2 ( n − 1 ) (D) n ( X ˉ − μ ) 2 n(\bar{X}-\mu)^{2} n ( X ˉ − μ ) 2 χ 2 \chi^{2} χ 2 ( i ) X ˉ ∼ N ( μ , σ 2 n ) \displaystyle \bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right) X ˉ ∼ N ( μ , n σ 2 ) X ˉ = 1 n ∑ i = 1 n X i ∼ N ( μ , 1 n ) \displaystyle \bar{X}=\frac{1}{n} \sum_{i=1}^n X_i \sim N\left(\mu, \frac{1}{n}\right) X ˉ = n 1 i = 1 ∑ n X i ∼ N ( μ , n 1 ) X ∼ N ( μ , 1 ) X ˉ ∼ N ( μ , 1 n ) X \sim N(\mu, 1) \quad \bar{X} \sim N\left(\mu, \frac{1}{n}\right) X ∼ N ( μ , 1 ) X ˉ ∼ N ( μ , n 1 ) 于是标准化后, X ˉ − μ 1 n = n ( X ˉ − μ ) ∼ N ( 0 , 1 ) \frac{\bar{X}-\mu}{\frac{1}{\sqrt{n}}}=\sqrt{n}(\bar{X}-\mu) \sim N(0,1) n 1 X ˉ − μ = n ( X ˉ − μ ) ∼ N ( 0 , 1 ) 从而 n ( X ˉ − μ ) 2 ∼ χ 2 ( 1 ) n(\bar{X}-\mu)^2 \sim \chi^2(1) n ( X ˉ − μ ) 2 ∼ χ 2 ( 1 ) 卡方分布的定义 (1) 设 X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X 1 , X 2 , ⋯ , X n N ( 0 , 1 ) N(0,1) N ( 0 , 1 ) χ 2 = X 1 2 + X 2 2 + ⋯ + X n 2 \chi^2=X_1^2+X_2^2+\cdots+X_n^2 χ 2 = X 1 2 + X 2 2 + ⋯ + X n 2 n n n χ 2 \chi^2 χ 2 χ 2 ∼ χ 2 ( n ) \chi^2 \sim \chi^2(n) χ 2 ∼ χ 2 ( n ) E ( χ 2 ) = n , D ( χ 2 ) = 2 n E\left(\chi^2\right)=n, D\left(\chi^2\right)=2 n E ( χ 2 ) = n , D ( χ 2 ) = 2 n 卡方分布可以理解为一堆相互独立的标准正态的平方相加 有多少个平方相加,就意味着它的自由度是多少 卡方分布的性质:设总体 X ∼ N ( μ , σ 2 ) , X 1 , X 2 , ⋯ , X n \displaystyle X \sim N\left(\mu, \sigma^2\right), X_1, X_2, \cdots, X_n X ∼ N ( μ , σ 2 ) , X 1 , X 2 , ⋯ , X n X X X X ˉ = 1 n ∑ i = 1 n X i , S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 \displaystyle \bar{X}=\frac{1}{n} \sum_{i=1}^n X_i, S^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 X ˉ = n 1 i = 1 ∑ n X i , S 2 = n − 1 1 i = 1 ∑ n ( X i − X ˉ ) 2 ( i ) X ˉ ∼ N ( μ , σ 2 n ) \displaystyle \bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right) X ˉ ∼ N ( μ , n σ 2 ) (ii) ( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \displaystyle \frac{(n-1) S^2}{\sigma^2} \sim \chi^2(n-1) σ 2 ( n − 1 ) S 2 ∼ χ 2 ( n − 1 ) (iii) X ˉ \bar{X} X ˉ S 2 S^2 S 2 二、填空题 (本题共 6 小题,每小题 4 分,共 24 分,把答案填在题中横线上. )
(9) 已知函数 f ( x ) = 1 1 + x 2 f(x)=\frac{1}{1+x^{2}} f ( x ) = 1 + x 2 1 f ( 3 ) ( 0 ) = f^{(3)}(0)= f ( 3 ) ( 0 ) =
泰勒展开:将 f ( x ) f(x) f ( x ) x = 0 x=0 x = 0 应用公式 f ( x ) = ∑ n = 0 ∞ f ( n ) ( 0 ) n ! x n \displaystyle f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} x^n f ( x ) = n = 0 ∑ ∞ n ! f ( n ) ( 0 ) x n 泰勒展开: \displaystyle 1 1 + x = 1 − x + x 2 + o ( x 2 ) ( x → 0 ) \frac{1}{1+x}=1-x+x^2+o\left(x^2\right)(x \rightarrow 0) 1 + x 1 = 1 − x + x 2 + o ( x 2 ) ( x → 0 ) f ( x ) = 1 1 + x 2 = 1 − x 2 + x 4 + o ( x 4 ) ( x → 0 ) . \displaystyle f(x)=\frac{1}{1+x^2}=1-x^2+x^4+o\left(x^4\right)(x \rightarrow 0) . f ( x ) = 1 + x 2 1 = 1 − x 2 + x 4 + o ( x 4 ) ( x → 0 ) . x 3 x^3 x 3 即 f ( 3 ) ( 0 ) 3 ! = 0 \frac{f^{(3)}(0)}{3!} = 0 3 ! f ( 3 ) ( 0 ) = 0 f ( 3 ) ( 0 ) = 0 f^{(3)}(0) = 0 f ( 3 ) ( 0 ) = 0 解 因为 f ( x ) = 1 1 + x 2 f(x)=\frac{1}{1+x^2} f ( x ) = 1 + x 2 1 则 f ′ ( x ) f^{\prime}(x) f ′ ( x ) f ′ ′ ( x ) f^{\prime \prime}(x) f ′′ ( x ) f ′ ′ ′ ( x ) f^{\prime \prime \prime}(x) f ′′′ ( x ) f ′ ′ ′ ( 0 ) = 0 f^{\prime \prime \prime}(0)=0 f ′′′ ( 0 ) = 0 (10) 微分方程 y ′ ′ + 2 y ′ + 3 y = 0 y^{\prime \prime}+2 y^{\prime}+3 y=0 y ′′ + 2 y ′ + 3 y = 0 y = y= y =
(10) 答 应填 e − x ( C 1 cos 2 x + C 2 sin 2 x ) \mathrm{e}^{-x}\left(C_1 \cos \sqrt{2} x+C_2 \sin \sqrt{2} x\right) e − x ( C 1 cos 2 x + C 2 sin 2 x ) C 1 , C 2 C_1, C_2 C 1 , C 2 该齐次 方程对应的特征方程为 r 2 + 2 r + 3 = 0 r^2+2 r+3=0 r 2 + 2 r + 3 = 0 解得 r 1 , 2 = − 1 ± 2 i r_{1,2}=-1 \pm \sqrt{2} \mathrm{i} r 1 , 2 = − 1 ± 2 i 套公式通解为 y = e − x ( C 1 cos 2 x + C 2 sin 2 x ) y=\mathrm{e}^{-x}\left(C_1 \cos \sqrt{2} x+C_2 \sin \sqrt{2} x\right) y = e − x ( C 1 cos 2 x + C 2 sin 2 x ) C 1 , C 2 C_1, C_2 C 1 , C 2 二阶常系数齐次线性微分方程 y ′ ′ + p y ′ + q y = 0 y^{\prime \prime}+p y^{\prime}+q y=0 y ′′ + p y ′ + q y = 0 p , q p, q p , q (1) 写出特征方程 λ 2 + p λ + q = 0 \lambda^2+p \lambda+q=0 λ 2 + p λ + q = 0 (2) 求出特征方程的两个根 λ 1 , λ 2 \lambda_1, \lambda_2 λ 1 , λ 2 (3) 根据特征方程两个根的不同情形,按照下述表格写出通解. 特征方程 λ 2 + p λ + q = 0 \lambda^2+p \lambda+q=0 λ 2 + p λ + q = 0 微分方程 y ′ ′ + p y ′ + q y = 0 y^{\prime \prime}+p y^{\prime}+q y=0 y ′′ + p y ′ + q y = 0 两个不相等的实根 λ 1 , λ 2 \lambda_1, \lambda_2 λ 1 , λ 2 y = C 1 e λ 1 x + C 2 e λ 2 x y=C_1 \mathrm{e}^{\lambda_1 x}+C_2 \mathrm{e}^{\lambda_2 x} y = C 1 e λ 1 x + C 2 e λ 2 x 两个相等的实根 λ 1 = λ 2 \lambda_1=\lambda_2 λ 1 = λ 2 y = ( C 1 + C 2 x ) e λ 1 x y=\left(C_1+C_2 x\right) \mathrm{e}^{\lambda_1 x} y = ( C 1 + C 2 x ) e λ 1 x 一对共轭复根 λ 1 , 2 = α ± β i \lambda_{1,2}=\alpha \pm \beta \mathrm{i} λ 1 , 2 = α ± β i y = e α x ( C 1 cos β x + C 2 sin β x ) y=\mathrm{e}^{\alpha x}\left(C_1 \cos \beta x+C_2 \sin \beta x\right) y = e αx ( C 1 cos β x + C 2 sin β x )
(11) 若曲线积分 ∫ L x d x − a y d y x 2 + y 2 − 1 \displaystyle \int_{L} \frac{x \mathrm{~d} x-a y \mathrm{~d} y}{x^{2}+y^{2}-1} ∫ L x 2 + y 2 − 1 x d x − a y d y D = { ( x , y ) ∣ x 2 + y 2 < 1 } D=\left\{(x, y) \mid x^{2}+y^{2}<1\right\} D = { ( x , y ) ∣ x 2 + y 2 < 1 } a a a
(11) 答 应填 -1 . 由曲线积分与路径无关知∂ Q ∂ x = ∂ P ∂ y \displaystyle \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} ∂ x ∂ Q = ∂ y ∂ P P = x x 2 + y 2 − 1 , Q = − a y x 2 + y 2 − 1 , \displaystyle P=\frac{x}{x^2+y^2-1}, Q=\frac{-a y}{x^2+y^2-1}, P = x 2 + y 2 − 1 x , Q = x 2 + y 2 − 1 − a y , ∂ P ∂ y = − 2 x y ( x 2 + y 2 − 1 ) 2 , ∂ Q ∂ x = 2 a x y ( x 2 + y 2 − 1 ) 2 . \displaystyle \frac{\partial P}{\partial y}=\frac{-2 x y}{\left(x^2+y^2-1\right)^2}, \frac{\partial Q}{\partial x}=\frac{2 a x y}{\left(x^2+y^2-1\right)^2} . ∂ y ∂ P = ( x 2 + y 2 − 1 ) 2 − 2 x y , ∂ x ∂ Q = ( x 2 + y 2 − 1 ) 2 2 a x y . \displaystyle ∂ P ∂ y = ∂ Q ∂ x \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x} ∂ y ∂ P = ∂ x ∂ Q − 2 x y ( x 2 + y 2 − 1 ) 2 = 2 a x y ( x 2 + y 2 − 1 ) 2 \frac{-2 x y}{\left(x^2+y^2-1\right)^2}=\frac{2 a x y}{\left(x^2+y^2-1\right)^2} ( x 2 + y 2 − 1 ) 2 − 2 x y = ( x 2 + y 2 − 1 ) 2 2 a x y − 2 x y = 2 a x y -2 x y=2 a x y − 2 x y = 2 a x y 解得 a = − 1 a=-1 a = − 1 设 G G G P ( x , y ) , Q ( x , y ) P(x, y), Q(x, y) P ( x , y ) , Q ( x , y ) G G G (1) 对于 G G G L , ∮ L P ( x , y ) d x + Q ( x , y ) d y = 0 L, \oint_L P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y=0 L , ∮ L P ( x , y ) d x + Q ( x , y ) d y = 0 (2) 曲线积分 ∫ L P ( x , y ) d x + Q ( x , y ) d y \displaystyle \int_L P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y ∫ L P ( x , y ) d x + Q ( x , y ) d y G G G (3) 存在 G G G U ( x , y ) U(x, y) U ( x , y ) d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y , \mathrm{d} U(x, y)=P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y , P ( x , y ) d x + Q ( x , y ) d y P(x, y) \mathrm{d} x+Q(x, y) \mathrm{d} y P ( x , y ) d x + Q ( x , y ) d y U ( x , y ) U(x, y) U ( x , y ) (4) 在 G G G ∂ P ∂ y = ∂ Q ∂ x \displaystyle \frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x} ∂ y ∂ P = ∂ x ∂ Q (12) 幂级数 ∑ n = 1 ∞ ( − 1 ) n − 1 n x n − 1 \displaystyle \sum_{n=1}^{\infty}(-1)^{n-1} n x^{n-1} n = 1 ∑ ∞ ( − 1 ) n − 1 n x n − 1 ( − 1 , 1 ) (-1,1) ( − 1 , 1 ) S ( x ) = S(x)= S ( x ) =
(12) 答 应填 1 ( 1 + x ) 2 \frac{1}{(1+x)^2} ( 1 + x ) 2 1 S ( x ) = ∑ n = 1 ∞ ( − 1 ) n − 1 n x n − 1 \displaystyle S(x)=\sum_{n=1}^{\infty}(-1)^{n-1} n x^{n-1} S ( x ) = n = 1 ∑ ∞ ( − 1 ) n − 1 n x n − 1 → 逐项积分 ∫ 0 x s ( t ) d t = ∫ 0 x ∑ n = 1 ∞ ( − 1 ) n − 1 n t n − 1 d t \displaystyle \xrightarrow[]{\text{逐项积分}}\int_0^x s(t) d t=\int_0^x \sum_{n=1}^{\infty}(-1)^{n-1} n t^{n-1} d t 逐项积分 ∫ 0 x s ( t ) d t = ∫ 0 x n = 1 ∑ ∞ ( − 1 ) n − 1 n t n − 1 d t \displaystyle \xlongequal[]{\text{提出求和∑}} \sum_{n=1}^{\infty} \int_0^x(-1)^{n-1} n t^{n-1} d t = 积分 ∑ n = 1 ∞ ( − 1 ) n − 1 x n = ∑ n = 0 ∞ ( − 1 ) n x n + 1 \displaystyle \xlongequal[]{\text{积分}} \sum_{n=1}^{\infty}(-1)^{n-1} x^n=\sum_{n=0}^{\infty}(-1)^n x^{n+1} 积分 n = 1 ∑ ∞ ( − 1 ) n − 1 x n = n = 0 ∑ ∞ ( − 1 ) n x n + 1 = 提出 x x ∑ n = 0 ∞ ( − 1 ) n x n = 级数转换 x 1 + x \displaystyle \xlongequal[]{\text{提出}x} x \sum_{n=0}^{\infty}(-1)^n x^n\xlongequal[]{\text{级数转换}}\frac{x}{1+x} 提出 x x n = 0 ∑ ∞ ( − 1 ) n x n 级数转换 1 + x x 1 1 + x = 1 − x + x 2 − ⋯ + ( − 1 ) n x n + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x n ( − 1 < x < 1 ) \displaystyle \frac{1}{1+x}=1-x+x^2-\cdots+(-1)^n x^n+\cdots=\sum_{n=0}^{\infty}(-1)^n x^n \quad(-1<x<1) 1 + x 1 = 1 − x + x 2 − ⋯ + ( − 1 ) n x n + ⋯ = n = 0 ∑ ∞ ( − 1 ) n x n ( − 1 < x < 1 ) (2012 年数一试题) ∑ n = 0 ∞ 4 n 2 + 4 n + 3 2 n + 1 x 2 n \displaystyle \sum_{n=0}^{\infty} \frac{4 n^2+4 n+3}{2 n+1} x^{2 n} n = 0 ∑ ∞ 2 n + 1 4 n 2 + 4 n + 3 x 2 n (2005 年数一试题) ∑ n = 1 ∞ ( − 1 ) n − 1 [ 1 + 1 n ( 2 n − 1 ) ] x 2 n \displaystyle \sum_{n=1}^{\infty}(-1)^{n-1}\left[1+\frac{1}{n(2 n-1)}\right] x^{2 n} n = 1 ∑ ∞ ( − 1 ) n − 1 [ 1 + n ( 2 n − 1 ) 1 ] x 2 n f ( x ) f(x) f ( x ) (13) 设矩阵 A = ( 1 0 1 1 1 2 0 1 1 ) , α 1 , α 2 , α 3 \displaystyle \boldsymbol{A}=\left(\begin{array}{lll}1 & 0 & 1 \\ 1 & 1 & 2 \\ 0 & 1 & 1\end{array}\right), \boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3} A = 1 1 0 0 1 1 1 2 1 , α 1 , α 2 , α 3 A α 1 , A α 2 , A α 3 \boldsymbol{A} \boldsymbol{\alpha}_{1}, \boldsymbol{A} \boldsymbol{\alpha}_{2}, \boldsymbol{A} \boldsymbol{\alpha}_{3} A α 1 , A α 2 , A α 3
(13) 读题 设矩阵 A = ( 1 0 1 1 1 2 0 1 1 ) , ⏟ 问的就是矩阵 A 的秩 \displaystyle \underbrace{\text{设矩阵} \boldsymbol{A}=\left(\begin{array}{lll}1 & 0 & 1 \\ 1 & 1 & 2 \\ 0 & 1 & 1\end{array}\right),}_{\text{问的就是矩阵}A\text{的秩}} 问的就是矩阵 A 的秩 设矩阵 A = 1 1 0 0 1 1 1 2 1 , α 1 , α 2 , α 3 为线性无关的 3 维列向量组 ⏟ 可逆 \displaystyle \underbrace{\begin{aligned}\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}\end{aligned}\text{为线性无关的} 3 \text{维列向量组}}_{\text{可逆}} 可逆 α 1 , α 2 , α 3 为线性无关的 3 维列向量组 A α 1 , A α 2 , A α 3 ⏟ 拆成矩阵乘法 \displaystyle \underbrace{\begin{aligned}\boldsymbol{A} \boldsymbol{\alpha}_{1}, \boldsymbol{A} \boldsymbol{\alpha}_{2}, \boldsymbol{A} \boldsymbol{\alpha}_{3}\end{aligned}}_{\text{拆成矩阵乘法}} 拆成矩阵乘法 A α 1 , A α 2 , A α 3 答 应填 2. 分析:本题主要考查求向量组的秩, 等价于求由向量组构成的矩阵的秩. 设 A \boldsymbol{A} A m × n m \times n m × n P , Q \boldsymbol{P}, \boldsymbol{Q} P , Q m m m n n n 则 r ( P A ) = r ( A Q ) = r ( A ) r(\boldsymbol{P A})=r(\boldsymbol{A} \boldsymbol{Q})=r(\boldsymbol{A}) r ( PA ) = r ( A Q ) = r ( A ) 解:由于 α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 ( α 1 , α 2 , α 3 ) \left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3\right) ( α 1 , α 2 , α 3 ) r ( A α 1 , A α 2 , A α 3 ) = r ( A ( α 1 , α 2 , α 3 ) ⏟ 可逆 ) = r ( A ) . r\left(\boldsymbol{A \boldsymbol { \alpha } _ { 1 }}, \boldsymbol{A} \boldsymbol{\alpha}_2, \boldsymbol{A} \boldsymbol{\alpha}_3\right)=r\left(\boldsymbol{A}\underbrace{\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3\right)}_{\text{可逆}}\right)=r(\boldsymbol{A}) . r ( A α 1 , A α 2 , A α 3 ) = r A 可逆 ( α 1 , α 2 , α 3 ) = r ( A ) . 一个矩阵乘以另一个可逆矩阵,不改变矩阵的秩 因此,只要找到矩阵A的秩,就可以求得向量组的秩 对矩阵 A \boldsymbol{A} A A = ( 1 0 1 1 1 2 0 1 1 ) → r 2 − r 1 ( 1 0 1 0 1 1 0 1 1 ) → r 3 − r 2 ∗ ( 1 0 1 0 1 1 0 0 0 ) . \displaystyle \boldsymbol{A}=\left(\begin{array}{lll}1 & 0 & 1 \\1 & 1 & 2 \\0 & 1 & 1\end{array}\right) \xrightarrow{r_2-r_1}\left(\begin{array}{lll}1 & 0 & 1 \\0 & 1 & 1 \\0 & 1 & 1\end{array}\right) \xrightarrow{r_3-r_2^*}\left(\begin{array}{lll}1 & 0 & 1 \\0 & 1 & 1 \\0 & 0 & 0\end{array}\right) . A = 1 1 0 0 1 1 1 2 1 r 2 − r 1 1 0 0 0 1 1 1 1 1 r 3 − r 2 ∗ 1 0 0 0 1 0 1 1 0 . 故 r ( A α 1 , A α 2 , A α 3 ) = r ( A ) = 2 r\left(\boldsymbol{A} \boldsymbol{\alpha}_1, \boldsymbol{A} \boldsymbol{\alpha}_2, \boldsymbol{A} \boldsymbol{\alpha}_3\right)=r(\boldsymbol{A})=2 r ( A α 1 , A α 2 , A α 3 ) = r ( A ) = 2 (14) 设随机变量 X X X F ( x ) = 0.5 Φ ( x ) + 0.5 Φ ( x − 4 2 ) F(x)=0.5 \Phi(x)+0.5 \Phi\left(\frac{x-4}{2}\right) F ( x ) = 0.5Φ ( x ) + 0.5Φ ( 2 x − 4 ) Φ ( x ) \Phi(x) Φ ( x ) E ( X ) = E(X)= E ( X ) =
(14) 由分布函数求得概率密度 分布函数为 F ( x ) = 0.5 Φ ( x ) + 0.5 Φ ( x − 4 2 ) → 概率密度 求导得 f ( x ) = F ′ ( x ) = 1 2 φ ( x ) + 1 4 φ ( x − 4 2 ) . F(x)=0.5 \Phi(x)+0.5 \Phi\left(\frac{x-4}{2}\right)\xrightarrow[\text{概率密度}]{\text{求导得}}f(x)=F^{\prime}(x)=\frac{1}{2} \varphi(x)+\frac{1}{4} \varphi\left(\frac{x-4}{2}\right) . F ( x ) = 0.5Φ ( x ) + 0.5Φ ( 2 x − 4 ) 求导得 概率密度 f ( x ) = F ′ ( x ) = 2 1 φ ( x ) + 4 1 φ ( 2 x − 4 ) . 在求谁的期望:就在谁前面乘上概率密度然后积分 E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x = 代入 f ( x ) 1 2 ∫ − ∞ + ∞ x φ ( x ) d x ⏟ = 0 + 1 4 ∫ − ∞ + ∞ x φ ( x − 4 2 ) d x ⏟ 换元求期望 \displaystyle E(X)=\int_{-\infty}^{+\infty} x f(x) \mathrm{d} x\xlongequal[]{\text{代入}f(x)}\frac{1}{2} \underbrace{\int_{-\infty}^{+\infty} x \varphi(x) \mathrm{d} x}_{=0}+\frac{1}{4} \underbrace{\int_{-\infty}^{+\infty} x \varphi\left(\frac{x-4}{2}\right) \mathrm{d} x}_{\text{换元求期望}} E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x 代入 f ( x ) 2 1 = 0 ∫ − ∞ + ∞ x φ ( x ) d x + 4 1 换元求期望 ∫ − ∞ + ∞ x φ ( 2 x − 4 ) d x 1 4 ∫ − ∞ + ∞ x φ ( x − 4 2 ) d → 1 4 拆成 1 2 × 1 2 x = d ( x − 4 2 ) = 1 2 d x . 线性凑微分 ∫ − ∞ + ∞ x − 4 + 4 2 φ ( x − 4 2 ) d ( x − 4 2 ) \displaystyle \frac{1}{4} \int_{-\infty}^{+\infty} x \varphi\left(\frac{x-4}{2}\right) \mathrm{d} \xrightarrow[]{\frac{1}{4}\text{拆成}\frac{1}{2}\times\frac{1}{2}}x\xlongequal[d\left(\frac{x-4}{2}\right)=\frac{1}{2} \mathrm{~d} x \text {. }]{\text{线性凑微分}}\int_{-\infty}^{+\infty} \frac{x-4+4}{2} \varphi\left(\frac{x-4}{2}\right) \mathrm{d}\left(\frac{x-4}{2}\right) 4 1 ∫ − ∞ + ∞ x φ ( 2 x − 4 ) d 4 1 拆成 2 1 × 2 1 x 线性凑微分 d ( 2 x − 4 ) = 2 1 d x . ∫ − ∞ + ∞ 2 x − 4 + 4 φ ( 2 x − 4 ) d ( 2 x − 4 ) = t x − 4 2 ∫ − ∞ + ∞ ( t + 2 ) φ ( t ) d t = 拆 ∫ − ∞ + ∞ t φ ( t ) d t ⏟ = 0 + 2 ∫ − ∞ + ∞ φ ( t ) d t ⏟ = 1 = 2 \displaystyle \xlongequal[]{t\frac{x-4}{2}}\int_{-\infty}^{+\infty}(t+2) \varphi(t) \mathrm{d} t\xlongequal[]{\text{拆}}\underbrace{\int_{-\infty}^{+\infty} t \varphi(t) \mathrm{d} t}_{=0}+2 \underbrace{\int_{-\infty}^{+\infty} \varphi(t) \mathrm{d} t}_{=1}=2 t 2 x − 4 ∫ − ∞ + ∞ ( t + 2 ) φ ( t ) d t 拆 = 0 ∫ − ∞ + ∞ tφ ( t ) d t + 2 = 1 ∫ − ∞ + ∞ φ ( t ) d t = 2 合并结果:E ( X ) = 0 + 2 = 2 E(X)=0+2=2 E ( X ) = 0 + 2 = 2 三、解答题 (本题共 9 小题,共 94 分,解答应写出文字说明、证明过程或演算步骤.)}
(15) (本题满分 10 分)f ( u , v ) f(u, v) f ( u , v ) y = f ( e x , cos x ) , 求 d y d x ∣ x = 0 , d 2 y d x 2 ∣ x = 0 ⏟ 对 x 连续求两次偏导,只能先求后代 \underbrace{y=f\left(\mathrm{e}^{x}, \cos x\right), \text{求} \left.\frac{\mathrm{d} y}{\mathrm{~d} x}\right|_{x=0},\left.\frac{\mathrm{d}^{2} y}{\mathrm{~d} x^{2}}\right|_{x=0}}_{\text{对}x\text{连续求两次偏导,只能先求后代}} 对 x 连续求两次偏导,只能先求后代 y = f ( e x , cos x ) , 求 d x d y x = 0 , d x 2 d 2 y x = 0
(15) 解 该问题涉及求函数 y = f ( e x , cos x ) y = f(\mathrm{e}^{x}, \cos x) y = f ( e x , cos x ) x = 0 x = 0 x = 0 计算函数 y = f ( e x , cos x ) y = f(\mathrm{e}^{x}, \cos x) y = f ( e x , cos x ) d y d x \frac{\mathrm{d} y}{\mathrm{d} x} d x d y 使用复合函数求导法则得:d y d x = f 1 ′ ⋅ e x + f 2 ′ ⋅ ( − sin x ) → 将 x = 0 代入得 d y d x ∣ x = 0 = f 1 ′ ( 1 , 1 ) \frac{\mathrm{d} y}{\mathrm{d} x} = f_1^{\prime} \cdot \mathrm{e}^x+f_2^{\prime} \cdot(-\sin x)\xrightarrow[]{\text{将}x=0\text{代入得}}\left.\frac{\mathrm{d} y}{\mathrm{~d} x}\right|_{x=0}=f_1^{\prime}(1,1) d x d y = f 1 ′ ⋅ e x + f 2 ′ ⋅ ( − sin x ) 将 x = 0 代入得 d x d y x = 0 = f 1 ′ ( 1 , 1 ) 利用导数乘法求二阶偏导,得d 2 y d x 2 = [ f 11 ′ ′ ⋅ e x + f 12 ′ ′ ⋅ ( − sin x ) ] e x + f 1 ′ ⋅ e x ⏟ f 1 ′ ⋅ e x 对 x 求偏导 − [ f 21 ′ ′ ⋅ e x + f 22 ′ ′ ⋅ ( − sin x ) ] sin x − f 2 ′ ⋅ cos x ⏟ f 2 ′ ⋅ ( − sin x ) 求偏导 \frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=\underbrace{\left[f_{11}^{\prime \prime} \cdot \mathrm{e}^x+f_{12}^{\prime \prime} \cdot(-\sin x)\right] \mathrm{e}^x+f_1^{\prime} \cdot \mathrm{e}^x}_{f_1^{\prime} \cdot \mathrm{e}^x\text{对}x\text{求偏导}}-\underbrace{\left[f_{21}^{\prime \prime} \cdot \mathrm{e}^x+f_{22}^{\prime \prime} \cdot(-\sin x)\right] \sin x-f_2^{\prime} \cdot \cos x}_{f_2^{\prime} \cdot(-\sin x)\text{求偏导}} d x 2 d 2 y = f 1 ′ ⋅ e x 对 x 求偏导 [ f 11 ′′ ⋅ e x + f 12 ′′ ⋅ ( − sin x ) ] e x + f 1 ′ ⋅ e x − f 2 ′ ⋅ ( − s i n x ) 求偏导 [ f 21 ′′ ⋅ e x + f 22 ′′ ⋅ ( − sin x ) ] sin x − f 2 ′ ⋅ cos x = 去括号,得 f 21 ′ ′ = f 12 ′ ′ f 11 ′ ′ ⋅ e 2 x + f 22 ′ ′ ⋅ sin 2 x + f 1 ′ ⋅ e x − f 2 ′ ⋅ cos x − 2 f 12 ′ ′ ⋅ sin x ⋅ e x , \xlongequal[\text{去括号,得}]{f_{21}^{\prime \prime}=f_{12}^{\prime \prime}}f_{11}^{\prime \prime} \cdot \mathrm{e}^{2 x}+f_{22}^{\prime \prime} \cdot \sin ^2 x+f_1^{\prime} \cdot \mathrm{e}^x-f_2^{\prime} \cdot \cos x-2 f_{12}^{\prime \prime} \cdot \sin x \cdot \mathrm{e}^x, \quad f 21 ′′ = f 12 ′′ 去括号,得 f 11 ′′ ⋅ e 2 x + f 22 ′′ ⋅ sin 2 x + f 1 ′ ⋅ e x − f 2 ′ ⋅ cos x − 2 f 12 ′′ ⋅ sin x ⋅ e x , 将x=0代入得d 2 y d x 2 ∣ x = 0 = f 11 ′ ′ ( 1 , 1 ) + f 1 ′ ( 1 , 1 ) − f 2 ′ ( 1 , 1 ) \left.\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}\right|_{x=0}=f_{11}^{\prime \prime}(1,1)+f_1^{\prime}(1,1)-f_2^{\prime}(1,1) d x 2 d 2 y x = 0 = f 11 ′′ ( 1 , 1 ) + f 1 ′ ( 1 , 1 ) − f 2 ′ ( 1 , 1 ) (16) (本题满分 10 分)lim n → ∞ ∑ k = 1 n k n 2 ln ( 1 + k n ) \displaystyle \lim _{n \rightarrow \infty} \sum_{k=1}^{n} \frac{k}{n^{2}} \ln \left(1+\frac{k}{n}\right) n → ∞ lim k = 1 ∑ n n 2 k ln ( 1 + n k )
(16) 解析这个数学题目,我们可以采用二叉树结构来详细地展示解题步骤:
问题: 求 lim n → ∞ ∑ k = 1 n k n 2 ln ( 1 + k n ) \displaystyle \lim _{n \rightarrow \infty} \sum_{k=1}^{n} \frac{k}{n^{2}} \ln \left(1+\frac{k}{n}\right) n → ∞ lim k = 1 ∑ n n 2 k ln ( 1 + n k ) 第一步:将数列和式极限转化为定积分 转化过程: 根据定积分的定义: I = lim n → ∞ 1 n ∑ k = 1 n k n ln ( 1 + k n ) = 1 n = d x i n = x ∫ 0 1 x ln ( 1 + x ) d x \displaystyle I =\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{k=1}^n \frac{k}{n} \ln \left(1+\frac{k}{n}\right) \xlongequal[\frac{1}{n}=d x]{\frac{i}{n}=x}\int_0^1 x \ln (1+x) \, \mathrm{d} x I = n → ∞ lim n 1 k = 1 ∑ n n k ln ( 1 + n k ) n i = x n 1 = d x ∫ 0 1 x ln ( 1 + x ) d x 为了分布积分,找出u和dv:x d x = 1 2 d ( x 2 ) x \, \mathrm{d} x = \frac{1}{2} \mathrm{d}(x^2) x d x = 2 1 d ( x 2 ) 第二步:化成udv形式,运用分部积分 I = 1 2 ∫ 0 1 ln ( 1 + x ) d ( x 2 ) = 分部 1 2 [ x 2 ln ( 1 + x ) ∣ 0 1 − ∫ 0 1 x 2 1 + x d x ] \displaystyle I = \frac{1}{2} \int_0^1 \ln (1+x) \, \mathrm{d}(x^2)\xlongequal[]{\text{分部}}\frac{1}{2} [\left. x^2 \ln (1+x)\right|_0 ^1-\int_0^1 \frac{x^2}{1+x} \mathrm{~d} x] I = 2 1 ∫ 0 1 ln ( 1 + x ) d ( x 2 ) 分部 2 1 [ x 2 ln ( 1 + x ) 0 1 − ∫ 0 1 1 + x x 2 d x ] 第一部分:x 2 ln ( 1 + x ) ∣ 0 1 = ln 2 − ln 1 = ln 2 \left. x^2 \ln (1+x)\right|_0 ^1=\ln 2-\ln 1=\ln 2 x 2 ln ( 1 + x ) 0 1 = ln 2 − ln 1 = ln 2 第二部分:∫ 0 1 x 2 1 + x d x = ∫ 0 1 x 2 + 1 − 1 1 + x d x \displaystyle \int_0^1 \frac{x^2}{1+x} \mathrm{~d} x=\int_0^1 \frac{x^2+1-1}{1+x} d x ∫ 0 1 1 + x x 2 d x = ∫ 0 1 1 + x x 2 + 1 − 1 d x 进行拆分得:= ∫ 0 1 x 2 + 1 1 + x d x − ∫ 0 1 1 1 + x d x = ∫ 0 1 ( x − 1 ) d ( x − 1 ) ⏟ ( x − 1 ) 2 2 ∣ 0 1 = − 1 2 − ∫ 0 1 1 1 + x d x ⏟ ln ( 1 + x ) ∣ 0 1 = ln 2 \displaystyle =\int_0^1 \frac{x^2+1}{1+x} d x-\int_0^1 \frac{1}{1+x} d x=\underbrace{\int_0^1(x-1) d(x-1)}_{\left.\frac{(x-1)^2}{2}\right|_0 ^1=-\frac12}-\underbrace{\int_0^1 \frac{1}{1+x} d x}_{\left.\ln (1+x)\right|_0 ^1=\ln 2} = ∫ 0 1 1 + x x 2 + 1 d x − ∫ 0 1 1 + x 1 d x = 2 ( x − 1 ) 2 0 1 = − 2 1 ∫ 0 1 ( x − 1 ) d ( x − 1 ) − l n ( 1 + x ) ∣ 0 1 = l n 2 ∫ 0 1 1 + x 1 d x 合并得:= 1 2 × [ ln 2 − ( − 1 2 + ln 2 ) ] = 1 2 × 1 2 = 1 4 =\frac{1}{2} \times\left[\ln 2-\left(-\frac{1}{2}+\ln 2\right)\right]=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4} = 2 1 × [ ln 2 − ( − 2 1 + ln 2 ) ] = 2 1 × 2 1 = 4 1 (17) (本题满分 10 分)y ( x ) y(x) y ( x ) 由方程 x 3 + y 3 − 3 x + 3 y − 2 = 0 确定 ⏟ 用条件极值或者拐点来判断 \underbrace{\text{由方程} x^{3}+y^{3}-3 x+3 y-2=0 \text{确定}}_{\text{用条件极值或者拐点来判断}} 用条件极值或者拐点来判断 由方程 x 3 + y 3 − 3 x + 3 y − 2 = 0 确定 y ( x ) y(x) y ( x )
(17) 求驻点 对方程两边同时对 x x x 3 x 2 + 3 y 2 y ′ − 3 + 3 y ′ = 0 3x^2 + 3y^2y' - 3 + 3y' = 0 3 x 2 + 3 y 2 y ′ − 3 + 3 y ′ = 0 令 y ′ = 0 y' = 0 y ′ = 0 x = ± 1 x = \pm 1 x = ± 1 将 x = 1 x = 1 x = 1 y 3 + 3 y − 4 = 0 y^3 + 3y - 4 = 0 y 3 + 3 y − 4 = 0 y = 1 y = 1 y = 1 将 x = − 1 x = -1 x = − 1 y 3 + 3 y = 0 y^3 + 3y = 0 y 3 + 3 y = 0 y = 0 y = 0 y = 0 得到两个驻点 x 1 = 1 x_1 = 1 x 1 = 1 x 2 = − 1 x_2 = -1 x 2 = − 1 判断驻点是否为极值点并求极值 对求导方程再次求导 6 x + 6 y ( y ′ ) 2 + 3 y 2 y ′ ′ + 3 y ′ ′ = 0 6x + 6y(y')^2 + 3y^2y'' + 3y'' = 0 6 x + 6 y ( y ′ ) 2 + 3 y 2 y ′′ + 3 y ′′ = 0 代入驻点 x 1 = 1 x_1 = 1 x 1 = 1 解得 y ′ ′ ( 1 ) = − 1 < 0 y''(1) = -1 < 0 y ′′ ( 1 ) = − 1 < 0 y ( x ) y(x) y ( x ) x = 1 x = 1 x = 1 y ( 1 ) = 1 y(1) = 1 y ( 1 ) = 1 代入驻点 x 2 = − 1 x_2 = -1 x 2 = − 1 解得 y ′ ′ ( − 1 ) = 2 > 0 y''(-1) = 2 > 0 y ′′ ( − 1 ) = 2 > 0 y ( x ) y(x) y ( x ) x = − 1 x = -1 x = − 1 y ( − 1 ) = 0 y(-1) = 0 y ( − 1 ) = 0 结论 y ( x ) y(x) y ( x ) x = 1 x = 1 x = 1 y ( 1 ) = 1 y(1) = 1 y ( 1 ) = 1 y ( x ) y(x) y ( x ) x = − 1 x = -1 x = − 1 y ( − 1 ) = 0 y(-1) = 0 y ( − 1 ) = 0 (18) (本题满分 10 分)f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ] 且 f ( 1 ) > 0 , lim x → 0 + f ( x ) x < 0. ⏟ 一正一负,零点定理 \displaystyle \underbrace{\text{且} f(1)>0, \lim _{x \rightarrow 0^{+}} \frac{f(x)}{x}<0.}_{\text{一正一负,零点定理}} 一正一负,零点定理 且 f ( 1 ) > 0 , x → 0 + lim x f ( x ) < 0. f ( x ) = 0 f(x)=0 f ( x ) = 0 ( 0 , 1 ) (0,1) ( 0 , 1 ) 方程 f ( x ) f ′ ′ ( x ) + [ f ′ ( x ) ] 2 = 0 ⏟ 对应乘法求导 \underbrace{\text{方程} f(x) f^{\prime \prime}(x)+\left[f^{\prime}(x)\right]^{2}=0}_{\text{对应乘法求导}} 对应乘法求导 方程 f ( x ) f ′′ ( x ) + [ f ′ ( x ) ] 2 = 0 ( 0 , 1 ) (0,1) ( 0 , 1 ) 至少存在两个不同实根 ⏟ 罗尔定理要找三个零点 \underbrace{\text{至少存在两个不同实根}}_{\text{罗尔定理要找三个零点}} 罗尔定理要找三个零点 至少存在两个不同实根
(18) 证明 (I) 方程 f ( x ) = 0 f(x)=0 f ( x ) = 0 ( 0 , 1 ) (0,1) ( 0 , 1 ) 已知f ( 1 ) > 0 f(1)>0 f ( 1 ) > 0 找另一个小于0的点 使用极限的保号性lim x → 0 + f ( x ) x < 0 \displaystyle \lim _{x \rightarrow 0^{+}} \frac{f(x)}{x}<0 x → 0 + lim x f ( x ) < 0 x = 0 x=0 x = 0 ( 0 , δ ) (0, \delta) ( 0 , δ ) 当 x ∈ ( 0 , δ ) x \in(0, \delta) x ∈ ( 0 , δ ) f ( x ) x < 0 \frac{f(x)}{x}<0 x f ( x ) < 0 存在 x 0 ∈ ( 0 , δ ) x_0 \in(0, \delta) x 0 ∈ ( 0 , δ ) f ( x 0 ) < 0 f(x_0)<0 f ( x 0 ) < 0 使用零点定理,由于刚才求得f ( x 0 ) < 0 f(x_0)<0 f ( x 0 ) < 0 f ( x 0 ) f ( 1 ) < 0 f(x_0) f(1)<0 f ( x 0 ) f ( 1 ) < 0 由零点定理,存在 c ∈ ( x 0 , 1 ) c \in(x_0, 1) c ∈ ( x 0 , 1 ) f ( c ) = 0 f(c)=0 f ( c ) = 0 f ( x ) = 0 f(x)=0 f ( x ) = 0 ( 0 , 1 ) (0,1) ( 0 , 1 ) (II) 方程 f ( x ) f ′ ′ ( x ) + [ f ′ ( x ) ] 2 = 0 f(x) f^{\prime \prime}(x)+[f^{\prime}(x)]^{2}=0 f ( x ) f ′′ ( x ) + [ f ′ ( x ) ] 2 = 0 ( 0 , 1 ) (0,1) ( 0 , 1 ) 构造辅助函数 令 F ( x ) = f ( x ) f ′ ( x ) F(x)=f(x) f^{\prime}(x) F ( x ) = f ( x ) f ′ ( x ) 导数关系:F ′ ( x ) = f ( x ) f ′ ′ ( x ) + [ f ′ ( x ) ] 2 F^{\prime}(x)=f(x) f^{\prime \prime}(x)+[f^{\prime}(x)]^2 F ′ ( x ) = f ( x ) f ′′ ( x ) + [ f ′ ( x ) ] 2 寻找三个零点: F ( 0 ) = f ( 0 ) ⋅ f ′ ( 0 ) = f ( 0 ) = 0 0 F(0)=f(0) \cdot f^{\prime}(0)\xlongequal[]{f(0)=0}0 F ( 0 ) = f ( 0 ) ⋅ f ′ ( 0 ) f ( 0 ) = 0 0 F ( c ) = f ( c ) ⋅ f ′ ( c ) = f ( c ) = 0 0 F(c)=f(c) \cdot f'(c)\xlongequal[]{f(c)=0}0 F ( c ) = f ( c ) ⋅ f ′ ( c ) f ( c ) = 0 0 第三个零点:f ( ξ ) = f ( ξ ) ⋅ f ′ ( ξ ) = f ′ ( ξ ) = 0 0 f(\xi)=f(\xi) \cdot f'(\xi)\xlongequal[]{f^{\prime}(\xi)=0}0 f ( ξ ) = f ( ξ ) ⋅ f ′ ( ξ ) f ′ ( ξ ) = 0 0 在 [ 0 , c ] [0, c] [ 0 , c ] f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 f ( c ) = 0 f(c)=0 f ( c ) = 0 存在 ξ ∈ ( 0 , c ) \xi \in(0, c) ξ ∈ ( 0 , c ) f ′ ( ξ ) = 0 f^{\prime}(\xi)=0 f ′ ( ξ ) = 0 根据三点 F F F F ( 0 ) = F ( ξ ) = F ( c ) = 0 F(0)=F(\xi)=F(c)=0 F ( 0 ) = F ( ξ ) = F ( c ) = 0 对 F ( x ) F(x) F ( x ) [ 0 , ξ ] [0, \xi] [ 0 , ξ ] 存在 ξ 1 ∈ ( 0 , ξ ) \xi_1 \in(0, \xi) ξ 1 ∈ ( 0 , ξ ) F ′ ( ξ 1 ) = 0 F^{\prime}(\xi_1)=0 F ′ ( ξ 1 ) = 0 对 F ( x ) F(x) F ( x ) [ ξ , c ] [\xi, c] [ ξ , c ] 存在 ξ 2 ∈ ( ξ , c ) \xi_2 \in(\xi, c) ξ 2 ∈ ( ξ , c ) F ′ ( ξ 2 ) = 0 F^{\prime}(\xi_2)=0 F ′ ( ξ 2 ) = 0 综上,方程 f ( x ) f ′ ′ ( x ) + [ f ′ ( x ) ] 2 = 0 f(x) f^{\prime \prime}(x)+[f^{\prime}(x)]^2=0 f ( x ) f ′′ ( x ) + [ f ′ ( x ) ] 2 = 0 ( 0 , 1 ) (0,1) ( 0 , 1 ) (19) (本题满分 10 分)S S S z = x 2 + y 2 z=\sqrt{x^{2}+y^{2}} z = x 2 + y 2 z 2 = 2 x z^{2}=2 x z 2 = 2 x μ ( x , y , z ) = 9 x 2 + y 2 + z 2 \mu(x, y, z)=9 \sqrt{x^{2}+y^{2}+z^{2}} μ ( x , y , z ) = 9 x 2 + y 2 + z 2 C C C C C C x O y x O y x O y S S S M M M 抽象题 )
(19) 读题 设薄片型物体 S S S 圆锥面 z = x 2 + y 2 被柱面 z 2 = 2 x 割下的有限部分 ⏟ 画图 \underbrace{\text{圆锥面} z=\sqrt{x^{2}+y^{2}} \text{被柱面} z^{2}=2 x \text{割下的有限部分}}_{\text{画图}} 画图 圆锥面 z = x 2 + y 2 被柱面 z 2 = 2 x 割下的有限部分 μ ( x , y , z ) = 9 x 2 + y 2 + z 2 \mu(x, y, z)=9 \sqrt{x^{2}+y^{2}+z^{2}} μ ( x , y , z ) = 9 x 2 + y 2 + z 2 圆雉面与柱面的交线为 C ⏟ 先求空间曲线 \underbrace{\text{圆雉面与柱面的交线为} C}_{\text{先求空间曲线}} 先求空间曲线 圆雉面与柱面的交线为 C 求 C 在 x O y 平面上的投影曲线的方程 ⏟ 令 z = 0 ,求得 x O y 面的投影 \underbrace{\text{求} C \text{在} x O y \text{平面上的投影曲线的方程}}_{\text{令}z=0\text{,求得}xOy\text{面的投影}} 令 z = 0 ,求得 x O y 面的投影 求 C 在 x O y 平面上的投影曲线的方程 求 S 的质量 M ⏟ 让你求 S 的曲面面积 \underbrace{\text{求} S \text{的质量} M}_{\text{让你求}S\text{的曲面面积}} 让你求 S 的曲面面积 求 S 的质量 M 抽象题 ) 注 正确写出投影曲线的方程 是后续的关键. ( I ) 由题设知, 圆锥面与柱面的交线 C C C { z = x 2 + y 2 , z 2 = 2 x , \displaystyle \left\{\begin{array}{l}z=\sqrt{x^2+y^2}, \\ z^2=2 x,\end{array}\right. { z = x 2 + y 2 , z 2 = 2 x , z z z x 2 + y 2 = x^2+y^2= x 2 + y 2 = 2 x 2 x 2 x 于是 C C C x O y x O y x O y { x 2 + y 2 = 2 x , z = 0. \displaystyle \left\{\begin{array}{l}x^2+y^2=2 x, \\z=0 .\end{array}\right. { x 2 + y 2 = 2 x , z = 0. (II) 因为 S S S μ ( x , y , z ) = 9 x 2 + y 2 + z 2 , \mu(x, y, z)=9 \sqrt{x^2+y^2+z^2}, μ ( x , y , z ) = 9 x 2 + y 2 + z 2 , S S S d S = 1 + z x 2 + z y 2 d x d y → z y = y z z x = x x 2 + y 2 = x z \displaystyle d S =\sqrt{1+z_x^2+z_y^2} d x d y \xrightarrow[z_y =\frac{y}{z}]{z_x =\frac{x}{\sqrt{x^2+y^2}}=\frac{x}{z}} d S = 1 + z x 2 + z y 2 d x d y z x = x 2 + y 2 x = z x z y = z y = 1 + x 2 z 2 + y 2 z 2 d x d y \displaystyle =\sqrt{1+\frac{x^2}{z^2}+\frac{y^2}{z^2}} d x d y = 1 + z 2 x 2 + z 2 y 2 d x d y = z 2 = x 2 + y 2 2 d x d y \displaystyle \xlongequal[]{z^2=x^2+y^2}\sqrt{2} d x d y z 2 = x 2 + y 2 2 d x d y 又 S S S x O y x O y x O y D = { ( x , y ) ∣ x 2 + y 2 ⩽ 2 x } , D=\left\{(x, y) \mid x^2+y^2 \leqslant 2 x\right\}, D = { ( x , y ) ∣ x 2 + y 2 ⩽ 2 x } , M = ∬ S 9 x 2 + y 2 + z 2 d S M=\iint_S 9 \sqrt{x^2+y^2+z^2} \mathrm{~d} S M = ∬ S 9 x 2 + y 2 + z 2 d S = z = x 2 + y 2 ∬ D 9 2 x 2 + y 2 ⋅ 2 d x d y \displaystyle \xlongequal[]{z=\sqrt{x^2+y^2}}\iint_D 9 \sqrt{2} \sqrt{x^2+y^2} \cdot \sqrt{2} d x d y z = x 2 + y 2 ∬ D 9 2 x 2 + y 2 ⋅ 2 d x d y = 18 ∬ x 2 + y 2 ⩽ 2 x x 2 + y 2 d x d y \displaystyle =18 \iint_{x^2+y^2 \leqslant 2 x} \sqrt{x^2+y^2} d x d y = 18 ∬ x 2 + y 2 ⩽ 2 x x 2 + y 2 d x d y = 18 ∫ − π 2 π 2 d θ ∫ 0 2 cos θ r ⋅ r d r \displaystyle =18 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \mathrm{~d} \theta \int_0^{2 \cos \theta} r \cdot r \mathrm{~d} r = 18 ∫ − 2 π 2 π d θ ∫ 0 2 c o s θ r ⋅ r d r = 48 ∫ − π 2 π 2 cos 3 θ d θ = 96 ∫ 0 π 2 cos 3 θ d θ \displaystyle =48 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos ^3 \theta \mathrm{~d} \theta=96 \int_0^{\frac{\pi}{2}} \cos ^3 \theta \mathrm{~d} \theta = 48 ∫ − 2 π 2 π cos 3 θ d θ = 96 ∫ 0 2 π cos 3 θ d θ = 96 × 2 3 = 64 \displaystyle =96 \times \frac{2}{3}=64 = 96 × 3 2 = 64 ∫ 0 π 2 sin n x d x = ∫ 0 π 2 cos n x d x = { n − 1 n ⋅ n − 3 n − 2 ⋯ ⋅ 1 2 ⋅ π 2 , n 为偶数, n ⩾ 2 , n − 1 n ⋅ n − 3 n − 2 ⋯ ⋅ 2 3 , n 为奇数, n ⩾ 3. \displaystyle \begin{aligned}\int_0^{\frac{\pi}{2}} \sin ^n x \mathrm{~d} x=\int_0^{\frac{\pi}{2}} \cos ^n x \mathrm{~d} x= \begin{cases}\frac{n-1}{n} \cdot \frac{n-3}{n-2} \cdots \cdot \frac{1}{2} \cdot \frac{\pi}{2}, & n \text { 为偶数, } n \geqslant 2, \\ \frac{n-1}{n} \cdot \frac{n-3}{n-2} \cdots \cdot \frac{2}{3}, & n \text { 为奇数, } n \geqslant 3 .\end{cases}\end{aligned} ∫ 0 2 π sin n x d x = ∫ 0 2 π cos n x d x = { n n − 1 ⋅ n − 2 n − 3 ⋯ ⋅ 2 1 ⋅ 2 π , n n − 1 ⋅ n − 2 n − 3 ⋯ ⋅ 3 2 , n 为偶数 , n ⩾ 2 , n 为奇数 , n ⩾ 3. (20) (本题满分 11 分)A = ( α 1 , α 2 , α 3 ) \boldsymbol{A}=\left(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}\right) A = ( α 1 , α 2 , α 3 ) α 3 = α 1 + 2 α 2 \boldsymbol{\alpha}_{3}=\boldsymbol{\alpha}_{1}+2 \boldsymbol{\alpha}_{2} α 3 = α 1 + 2 α 2 r ( A ) = 2 r(\boldsymbol{A})=2 r ( A ) = 2 β = α 1 + α 2 + α 3 \boldsymbol{\beta}=\boldsymbol{\alpha}_{1}+\boldsymbol{\alpha}_{2}+\boldsymbol{\alpha}_{3} β = α 1 + α 2 + α 3 A x = β \boldsymbol{A x}=\boldsymbol{\beta} Ax = β
(20) 读题:设 3 阶矩阵 A = ( α 1 , α 2 , α 3 ) \boldsymbol{A}=\left(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}\right) A = ( α 1 , α 2 , α 3 ) 有 3 个不同的特征值 ⏟ 特征值一个是 0 ,其他两个不是 0 \underbrace{\text{有} 3 \text{个不同的特征值}}_{\text{特征值一个是}0\text{,其他两个不是}0} 特征值一个是 0 ,其他两个不是 0 有 3 个不同的特征值 α 3 = α 1 + 2 α 2 ⏟ 得出齐次的通解 \underbrace{\boldsymbol{\alpha}_{3}=\boldsymbol{\alpha}_{1}+2 \boldsymbol{\alpha}_{2}}_{\text{得出齐次的通解}} 得出齐次的通解 α 3 = α 1 + 2 α 2 r ( A ) = 2 ⏟ 有一个特征值是 0 \underbrace{r(\boldsymbol{A})=2}_{\text{有一个特征值是}0} 有一个特征值是 0 r ( A ) = 2 β = α 1 + α 2 + α 3 ⏟ 得出非齐次的特解 \underbrace{\boldsymbol{\beta}=\boldsymbol{\alpha}_{1}+\boldsymbol{\alpha}_{2}+\boldsymbol{\alpha}_{3}}_{\text{得出非齐次的特解}} 得出非齐次的特解 β = α 1 + α 2 + α 3 方程组 A x = β 的通解 ⏟ 齐次通解 + 非齐次特解 \underbrace{\text{方程组} \boldsymbol{A x}=\boldsymbol{\beta} \text{的通解}}_{\text{齐次通解}+\text{非齐次特解}} 齐次通解 + 非齐次特解 方程组 Ax = β 的通解 分析 本题综合考查了行列式与特征值的关系以及解线性方程组. 第( I ) 问要证明 A \boldsymbol{A} A A \boldsymbol{A} A 第 (II) 问主要考查解线性方程组. (I)由于 A \boldsymbol{A} A λ 1 , λ 2 , λ 3 \lambda_1, \lambda_2, \lambda_3 λ 1 , λ 2 , λ 3 该对角矩阵的秩 ⩾ 2 \geqslant 2 ⩾ 2 r ( A ) ⩾ 2 r(\boldsymbol{A}) \geqslant 2 r ( A ) ⩾ 2 又因为 α 3 = α 1 + 2 α 2 \boldsymbol{\alpha}_3=\boldsymbol{\alpha}_1+2 \boldsymbol{\alpha}_2 α 3 = α 1 + 2 α 2 α 1 , α 2 , α 3 \boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3 α 1 , α 2 , α 3 ∣ A ∣ = 0 |\boldsymbol{A}|=0 ∣ A ∣ = 0 该对角矩阵的秩 < 3 \text{<} 3 < 3 r ( A ) < 3 r(\boldsymbol{A}) \text{<} 3 r ( A ) < 3 因此, r ( A ) = 2 r(\boldsymbol{A})=2 r ( A ) = 2 α 1 + 2 α 2 − α 3 = 0 → 写成矩阵乘法 ( α 1 , α 2 , α 3 ) ( 1 2 − 1 ) = 0 A ( 1 2 − 1 ) = 0 \displaystyle \alpha_1+2 \alpha_2-\alpha_3=0 \xrightarrow[]{\text{写成矩阵乘法}}\left(\alpha_1, \alpha_2, \alpha_3\right)\left(\begin{array}{c}1 \\2 \\-1\end{array}\right)=0 \quad A\left(\begin{array}{c}1 \\2 \\-1\end{array}\right)=0 α 1 + 2 α 2 − α 3 = 0 写成矩阵乘法 ( α 1 , α 2 , α 3 ) 1 2 − 1 = 0 A 1 2 − 1 = 0 又 r ( A ) = 2 r(\boldsymbol{A})=2 r ( A ) = 2 A x = 0 \displaystyle Ax=0 A x = 0 所以 ( 1 2 − 1 ) \displaystyle \left(\begin{array}{c}1 \\ 2 \\ -1\end{array}\right) 1 2 − 1 A x = 0 \boldsymbol{A x}=\mathbf{0} Ax = 0 β = α 1 + α 2 + α 3 → 写成矩阵乘法 ( α 1 , α 2 , α 3 ) ( 1 1 1 ) = β A ( 1 1 1 ) = β \displaystyle \beta=\alpha_1+\alpha_2+\alpha_3 \xrightarrow[]{\text{写成矩阵乘法}}\left(\alpha_1, \alpha_2 ,\alpha_3\right)\left(\begin{array}{c}1 \\1 \\1\end{array}\right)=\beta \quad A\left(\begin{array}{l}1 \\1 \\1\end{array}\right)=\beta β = α 1 + α 2 + α 3 写成矩阵乘法 ( α 1 , α 2 , α 3 ) 1 1 1 = β A 1 1 1 = β 所以 ( 1 1 1 ) \displaystyle \left(\begin{array}{l}1 \\ 1 \\ 1\end{array}\right) 1 1 1 A x = β \boldsymbol{A x}=\boldsymbol{\beta} Ax = β A x = β \displaystyle A x=\beta A x = β x = ( 1 1 1 ) + k 1 ( 1 − 1 ) \displaystyle x=\left(\begin{array}{l}1 \\1 \\1\end{array}\right)+k_1\binom{1}{-1} x = 1 1 1 + k 1 ( − 1 1 ) k k k (21) (本题满分 11 分)f ( x 1 , x 2 , x 3 ) = 2 x 1 2 − x 2 2 + a x 3 2 + 2 x 1 x 2 − 8 x 1 x 3 + 2 x 2 x 3 f\left(x_{1}, x_{2}, x_{3}\right)=2 x_{1}^{2}-x_{2}^{2}+a x_{3}^{2}+2 x_{1} x_{2}-8 x_{1} x_{3}+2 x_{2} x_{3} f ( x 1 , x 2 , x 3 ) = 2 x 1 2 − x 2 2 + a x 3 2 + 2 x 1 x 2 − 8 x 1 x 3 + 2 x 2 x 3 x = Q y \boldsymbol{x}=\boldsymbol{Q y} x = Qy λ 1 y 1 2 + λ 2 y 2 2 \lambda_{1} y_{1}^{2}+\lambda_{2} y_{2}^{2} λ 1 y 1 2 + λ 2 y 2 2 a a a Q \boldsymbol{Q} Q
(21) 读题 设二次型 f ( x 1 , x 2 , x 3 ) = 2 x 1 2 − x 2 2 + a x 3 2 + 2 x 1 x 2 − 8 x 1 x 3 + 2 x 2 x 3 ⏟ 先化为实对称矩阵 \underbrace{f\left(x_{1}, x_{2}, x_{3}\right)=2 x_{1}^{2}-x_{2}^{2}+a x_{3}^{2}+2 x_{1} x_{2}-8 x_{1} x_{3}+2 x_{2} x_{3}}_{\text{先化为实对称矩阵}} 先化为实对称矩阵 f ( x 1 , x 2 , x 3 ) = 2 x 1 2 − x 2 2 + a x 3 2 + 2 x 1 x 2 − 8 x 1 x 3 + 2 x 2 x 3 x = Q y \boldsymbol{x}=\boldsymbol{Q y} x = Qy 标准形为 λ 1 y 1 2 + λ 2 y 2 2 ⏟ 有个特征值为 0 ,行列式为 0 \underbrace{\text{标准形为} \lambda_{1} y_{1}^{2}+\lambda_{2} y_{2}^{2}}_{\text{有个特征值为}0\text{,行列式为}0} 有个特征值为 0 ,行列式为 0 标准形为 λ 1 y 1 2 + λ 2 y 2 2 求 a 的值 ⏟ 用 ∣ A ∣ = 0 求 \underbrace{\text{求} a \text{的值}}_{\text{用}|A|=0\text{求}} 用 ∣ A ∣ = 0 求 求 a 的值 一个正交矩阵 Q ⏟ A 的特征向量单位化拼成 Q \underbrace{\text{一个正交矩阵} \boldsymbol{Q}}_{A\text{的特征向量单位化拼成}Q} A 的特征向量单位化拼成 Q 一个正交矩阵 Q 二次型都可以转化为实对称矩阵的问题 二次型 f f f A = ( 2 1 − 4 1 − 1 1 − 4 1 a ) \displaystyle \boldsymbol{A}=\left(\begin{array}{ccc}2 & 1 & -4 \\1 & -1 & 1 \\-4 & 1 & a\end{array}\right) A = 2 1 − 4 1 − 1 1 − 4 1 a 由于 f f f x = Q y \boldsymbol{x}=\boldsymbol{Q} \boldsymbol{y} x = Q y λ 1 y 1 2 + λ 2 y 2 2 \lambda_1 y_1^2+\lambda_2 y_2^2 λ 1 y 1 2 + λ 2 y 2 2 故 A \boldsymbol{A} A λ 1 , λ 2 , 0 \lambda_1, \lambda_2, 0 λ 1 , λ 2 , 0 ∣ A ∣ = 0 |\boldsymbol{A}|=0 ∣ A ∣ = 0 求行列式的值 ∣ A ∣ = ∣ 21 − 4 1 − 11 − 41 a ∣ = r 4 + 4 r 1 r 1 − 2 r 2 ∣ 03 − 6 1 − 11 0 − 39 + 4 ∣ = ( − 1 ) 2 + 1 × 1 × ∣ 3 − 6 − 3 a + 4 ∣ \displaystyle |\boldsymbol{A}| =\left|\begin{array}{ccc}2 1 -4 \\1 -1 1 \\-4 1 a\end{array}\right|\xlongequal[r4+4r1]{r1-2r2}\left|\begin{array}{ccc}0 3 -6 \\1 -1 1 \\0 -3 9+4\end{array}\right|=(-1)^{2+1} \times 1 \times\left|\begin{array}{cc}3 -6 \\-3 a+4\end{array}\right| ∣ A ∣ = 21 − 4 1 − 11 − 41 a r 1 − 2 r 2 r 4 + 4 r 1 03 − 6 1 − 11 0 − 39 + 4 = ( − 1 ) 2 + 1 × 1 × 3 − 6 − 3 a + 4 = − 1 × ∣ 3 − 6 0 a − 2 ∣ = − 3 ( a − 2 ) . \displaystyle =-1 \times\left|\begin{array}{cc}3 -6 \\0 a-2\end{array}\right|=-3(a-2) . = − 1 × 3 − 6 0 a − 2 = − 3 ( a − 2 ) . 由题设知 ∣ A ∣ = 0 |\boldsymbol{A}|=0 ∣ A ∣ = 0 a = 2 a=2 a = 2 ∣ A − λ E ∣ = ∣ 2 − λ 1 − 4 1 − 1 − λ 1 − 412 − λ ∣ = ∣ 6 − λ 1 − 4 0 − 1 − λ 1 λ − 612 − λ ∣ = ∣ 6 − λ 1 − 4 0 − 1 − λ 1 02 − 2 − λ ∣ \displaystyle |A-\lambda E|=\left|\begin{array}{ccc}2-\lambda 1 -4 \\1 -1-\lambda 1 \\-4 1 2-\lambda\end{array}\right|=\left|\begin{array}{ccc}6-\lambda 1 -4 \\0 -1-\lambda 1 \\\lambda-6 1 2-\lambda\end{array}\right|=\left|\begin{array}{ccc}6-\lambda 1 -4 \\0 -1-\lambda 1 \\0 2 -2-\lambda\end{array}\right| ∣ A − λ E ∣ = 2 − λ 1 − 4 1 − 1 − λ 1 − 412 − λ = 6 − λ 1 − 4 0 − 1 − λ 1 λ − 612 − λ = 6 − λ 1 − 4 0 − 1 − λ 1 02 − 2 − λ = ( 6 − λ ) [ λ 2 + 3 λ + 2 − 2 ] = ( 6 − λ ) ( λ + 3 ) λ = 0 \displaystyle =(6-\lambda)\left[\lambda^2+3 \lambda+2-2\right]=(6-\lambda)(\lambda+3) \lambda=0 = ( 6 − λ ) [ λ 2 + 3 λ + 2 − 2 ] = ( 6 − λ ) ( λ + 3 ) λ = 0 所以特征值为 λ 1 = − 3 , λ 2 = 6 , λ 3 = 0 \lambda_1=-3, \lambda_2=6, \lambda_3=0 λ 1 = − 3 , λ 2 = 6 , λ 3 = 0 求特征值对应的特征向量 6 E − A = ( 4 − 14 − 17 − 1 4 − 14 ) → r 3 − r 1 ( 4 − 14 − 17 − 1 000 ) → r 1 + 4 r 2 ( 0270 − 17 − 1 000 ) \displaystyle 6 \boldsymbol{E}-\boldsymbol{A}=\left(\begin{array}{ccc}4 -1 4 \\ -1 7 -1 \\ 4 -1 4\end{array}\right) \xrightarrow[]{r3-r1}\left(\begin{array}{ccc}4 -1 4 \\ -1 7 -1 \\ 0 0 0\end{array}\right)\xrightarrow[]{r1+4r2}\left(\begin{array}{ccc}0 27 0 \\ -1 7 -1 \\ 0 0 0\end{array}\right) 6 E − A = 4 − 14 − 17 − 1 4 − 14 r 3 − r 1 4 − 14 − 17 − 1 000 r 1 + 4 r 2 0270 − 17 − 1 000 → r 1 ∗ × 1 27 ( 0 1 0 1 − 7 1 0 0 0 ) → r 2 − 7 r 1 ∗ ∗ ( 0 1 0 1 0 1 0 0 0 ) \displaystyle \xrightarrow[]{r_1^* \times \frac{1}{27}}\left(\begin{array}{ccc}0 & 1 & 0 \\ 1 & -7 & 1 \\ 0 & 0 & 0\end{array}\right) \xrightarrow[]{r_2-7 r_1^{* *}}\left(\begin{array}{lll}0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 0 & 0\end{array}\right) r 1 ∗ × 27 1 0 1 0 1 − 7 0 0 1 0 r 2 − 7 r 1 ∗∗ 0 1 0 1 0 0 0 1 0 { x 2 = 0 x 1 + x 3 = 0 { x 1 = k 1 x 2 = 0 x 3 = − k 1 x = k 1 ( 1 0 − 1 ) ( k 1 ≠ 0 ) \displaystyle \left\{\begin{array} { r l } { x _ { 2 } } & { = 0 }\\{ x _ { 1 } + x _ { 3 } } & { = 0 } \end{array} \quad \left\{\begin{array}{l}x_1=k_1 \\x_2=0 \\x_3=-k_1\end{array} \quad x=k_1\left(\begin{array}{c}1 \\0 \\-1\end{array}\right)\left(k_1 \neq 0\right)\right.\right. ⎩ ⎨ ⎧ x 2 x 1 + x 3 = 0 = 0 ⎩ ⎨ ⎧ x 1 = k 1 x 2 = 0 x 3 = − k 1 x = k 1 1 0 − 1 ( k 1 = 0 ) 单位特征向量为 β 2 = 1 2 ( − 1 , 0 , 1 ) T \boldsymbol{\beta}_2=\frac{1}{\sqrt{2}}(-1,0,1)^{\mathrm{T}} β 2 = 2 1 ( − 1 , 0 , 1 ) T − 3 E − A = ( − 5 − 14 − 1 − 2 − 1 4 − 1 − 5 ) → r 3 + r 1 ( − 5 − 14 − 1 − 2 − 1 − 1 − 2 − 1 ) → r 3 ∗ − r 2 ( − 5 − 14 − 1 − 2 − 1 000 ) \displaystyle -3 \boldsymbol{E}-\boldsymbol{A} =\left(\begin{array}{ccc}-5 -1 4 \\-1 -2 -1 \\4 -1 -5\end{array}\right) \xrightarrow[]{r_3+r_1}\left(\begin{array}{ccc}-5 -1 4 \\ -1 -2 -1 \\ -1 -2 -1\end{array}\right)\xrightarrow[r_3^*-r_2]{}\left(\begin{array}{ccc}-5 -1 4 \\-1 -2 -1 \\0 0 0\end{array}\right) − 3 E − A = − 5 − 14 − 1 − 2 − 1 4 − 1 − 5 r 3 + r 1 − 5 − 14 − 1 − 2 − 1 − 1 − 2 − 1 r 3 ∗ − r 2 − 5 − 14 − 1 − 2 − 1 000 → r 1 − 5 r 2 ( 0 9 9 − 1 − 2 − 1 0 0 0 ) → r 2 × ( − 1 ) ( 0 9 9 1 2 1 0 0 0 ) \displaystyle \xrightarrow[]{r_1-5 r_2}\left(\begin{array}{ccc}0 & 9 & 9 \\ -1 & -2 & -1 \\ 0 & 0 & 0\end{array}\right)\xrightarrow[r_2 \times(-1)]{}\left(\begin{array}{lll}0 & 9 & 9 \\1 & 2 & 1 \\0 & 0 & 0\end{array}\right) r 1 − 5 r 2 0 − 1 0 9 − 2 0 9 − 1 0 r 2 × ( − 1 ) 0 1 0 9 2 0 9 1 0 → r 2 ∗ − r 1 ∗ ∗ r 1 ∗ × 1 9 ( 011 110 000 ) . \displaystyle \xrightarrow[r_2^*-r_1^{* *}]{r_1^* \times \frac{1}{9}}\left(\begin{array}{lll}0 1 1 \\1 1 0 \\0 0 0\end{array}\right) . r 1 ∗ × 9 1 r 2 ∗ − r 1 ∗∗ 011 110 000 . { x 2 + x 3 = 0 x 1 + x 2 = 0 \displaystyle \left\{\begin{array}{l}x_2+x_3=0 \\ x_1+x_2=0\end{array}\right. { x 2 + x 3 = 0 x 1 + x 2 = 0 ( − 3 E − A ) x = 0 (-3 \boldsymbol{E}-\boldsymbol{A}) \boldsymbol{x}=\boldsymbol{0} ( − 3 E − A ) x = 0 η 2 = ( 1 , − 1 , 1 ) T \boldsymbol{\eta}_2=(1,-1,1)^{\mathrm{T}} η 2 = ( 1 , − 1 , 1 ) T 单位特征向量为 β 1 = 1 3 ( 1 , − 1 , 1 ) T \beta_1=\frac{1}{\sqrt{3}}(1,-1,1)^{\mathrm{T}} β 1 = 3 1 ( 1 , − 1 , 1 ) T \displaystyle λ = 0 \lambda=0 λ = 0 0 E − A = ( − 2 − 14 − 11 − 1 4 − 1 − 2 ) → r 3 + 2 r 1 ( − 2 − 14 − 11 − 1 000 ) 0 \boldsymbol{E}-\boldsymbol{A}=\left(\begin{array}{ccc}-2 -1 4 \\-1 1 -1 \\4 -1 -2\end{array}\right) \xrightarrow[]{r3+2r1}\left(\begin{array}{ccc}-2 -1 4 \\-1 1 -1 \\0 0 0\end{array}\right) 0 E − A = − 2 − 14 − 11 − 1 4 − 1 − 2 r 3 + 2 r 1 − 2 − 14 − 11 − 1 000 → r 1 − 2 r 2 ( 0 − 36 − 11 − 1 000 ) → r 1 ∗ × ( − 1 3 ) ( 01 − 2 1 − 11 000 ) → r 2 + r 1 ( 01 − 2 10 − 1 000 ) \displaystyle \xrightarrow[]{r1-2r2}\left(\begin{array}{ccc}0 -3 6 \\-1 1 -1 \\0 0 0\end{array}\right) \xrightarrow[]{r_1^* \times\left(-\frac{1}{3}\right)}\left(\begin{array}{ccc}0 1 -2 \\1 -1 1 \\0 0 0\end{array}\right) \xrightarrow[]{r2+r1}\left(\begin{array}{ccc}0 1 -2 \\1 0 -1 \\0 0 0\end{array}\right) r 1 − 2 r 2 0 − 36 − 11 − 1 000 r 1 ∗ × ( − 3 1 ) 01 − 2 1 − 11 000 r 2 + r 1 01 − 2 10 − 1 000 { x 2 − 2 x 3 = 0 x 1 − x 3 = 0 \displaystyle \left\{\begin{array}{l}x_2-2 x_3=0 \\ x_1-x_3=0\end{array}\right. { x 2 − 2 x 3 = 0 x 1 − x 3 = 0 ( 0 E − A ) x = 0 (0 \boldsymbol{E}-\boldsymbol{A}) \boldsymbol{x}=\boldsymbol{0} ( 0 E − A ) x = 0 η 3 = ( 1 , 2 , 1 ) T \boldsymbol{\eta}_3=(1,2,1)^{\mathrm{T}} η 3 = ( 1 , 2 , 1 ) T 单位特征向量为 β 3 = 1 6 ( 1 , 2 , 1 ) T \boldsymbol{\beta}_3=\frac{1}{\sqrt{6}}(1,2,1)^{\mathrm{T}} β 3 = 6 1 ( 1 , 2 , 1 ) T 故所求的一个正交矩阵为 Q = ( β 1 , β 2 , β 3 ) = ( 1 3 − 1 2 1 6 − 1 3 0 2 6 1 3 1 2 1 6 ) \displaystyle Q=\left(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3\right)=\left(\begin{array}{ccc}\frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} \\ -\frac{1}{\sqrt{3}} & 0 & \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}}\end{array}\right) Q = ( β 1 , β 2 , β 3 ) = 3 1 − 3 1 3 1 − 2 1 0 2 1 6 1 6 2 6 1 (22) (本题满分 11 分)X , Y X, Y X , Y X X X P { X = 0 } = P { X = 2 } = 1 2 , Y P\{X=0\}=P\{X=2\}=\frac{1}{2}, Y P { X = 0 } = P { X = 2 } = 2 1 , Y f ( y ) = { 2 y , 0 < y < 1 , 0 , 其他. \displaystyle f(y)= \begin{cases}2 y, & 0<y<1, \\ 0, & \text { 其他. }\end{cases} f ( y ) = { 2 y , 0 , 0 < y < 1 , 其他 . P { Y ⩽ E ( Y ) } P\{Y \leqslant E(Y)\} P { Y ⩽ E ( Y )} Z = X + Y Z=X+Y Z = X + Y
(22) 读题X , Y X, Y X , Y X X X P { X = 0 } = P { X = 2 } = 1 2 P\{X=0\}=P\{X=2\}=\frac{1}{2} P { X = 0 } = P { X = 2 } = 2 1 Y 的概率密度为 f ( y ) = { 2 y , 0 < y < 1 , 0 , 其他. ⏟ 用来求 Y 的期望 \displaystyle \underbrace{Y\text{的概率密度为} f(y)= \begin{cases}2 y, & 0<y<1, \\ 0, & \text { 其他. }\end{cases}}_{\text{用来求}Y\text{的期望}} 用来求 Y 的期望 Y 的概率密度为 f ( y ) = { 2 y , 0 , 0 < y < 1 , 其他 . P { Y ⩽ E ( Y ) } ⏟ 要求 E ( Y ) ,要会连续型概率公式 \underbrace{P\{Y \leqslant E(Y)\}}_{\text{要求}E(Y)\text{,要会连续型概率公式}} 要求 E ( Y ) ,要会连续型概率公式 P { Y ⩽ E ( Y )} Z = X + Y 的概率密度 ⏟ 先用全集分解求混合型的分布函数 \underbrace{Z=X+Y \text{的概率密度}}_{\text{先用全集分解求混合型的分布函数}} 先用全集分解求混合型的分布函数 Z = X + Y 的概率密度 由于 X X X 故不能利用 X , Y X, Y X , Y Z = X + Y Z=X+Y Z = X + Y 卷积公式 ), 只能按定义先求其分布函数, 再求概率密度.P { Y ⩽ E ( Y ) } P\{Y \leqslant E(Y)\} P { Y ⩽ E ( Y )} 计算 E ( Y ) E(Y) E ( Y ) E ( Y ) = ∫ − ∞ + ∞ y f ( y ) d y = ∫ 0 1 y \cdotp 2 y d y = ∫ 0 1 2 y 2 d y = 2 3 y 3 ∣ 0 1 = 2 3 \displaystyle E(Y) = \int_{-\infty}^{+\infty} y f(y) dy=\int_0^1 y\text{·}2 y d y=\int_0^1 2y^2 dy =\left.\frac{2}{3} y^3\right|_0 ^1= \frac{2}{3} E ( Y ) = ∫ − ∞ + ∞ y f ( y ) d y = ∫ 0 1 y \cdotp 2 y d y = ∫ 0 1 2 y 2 d y = 3 2 y 3 0 1 = 3 2 将E ( Y ) E(Y) E ( Y ) P { Y ⩽ E ( Y ) } P\{Y \leqslant E(Y)\} P { Y ⩽ E ( Y )} P { Y ⩽ E ( Y ) } = P { Y ⩽ 2 3 } = ∫ − ∞ 2 3 f ( y ) d y = ∫ 0 2 3 2 y d y = y 2 ∣ 0 2 3 = 4 9 \displaystyle P\{Y \leqslant E(Y)\} = P\left\{Y \leqslant \frac{2}{3}\right\}=\int_{-\infty}^{\frac{2}{3}} f(y) d y= \int_0^{\frac{2}{3}} 2y dy =\left.y^2\right|_0 ^{\frac{2}{3}}=\frac{4}{9} P { Y ⩽ E ( Y )} = P { Y ⩽ 3 2 } = ∫ − ∞ 3 2 f ( y ) d y = ∫ 0 3 2 2 y d y = y 2 0 3 2 = 9 4 Z = X + Y Z=X+Y Z = X + Y 先求Z Z Z F Z ( z ) F_Z(z) F Z ( z ) F Z ( z ) = P { Z ⩽ z } = P { X + Y ⩽ z } F_Z(z) = P\{Z \leqslant z\} = P\{X+Y \leqslant z\} F Z ( z ) = P { Z ⩽ z } = P { X + Y ⩽ z } = 全集分解 对离散的进行 P { X + Y ⩽ z , X = 0 } + P { X + Y ⩽ z , X = 2 } \xlongequal[\text{全集分解}]{\text{对离散的进行}}P\{X+Y \leqslant z , X=0\} + P\{X+Y \leqslant z , X=2\} 对离散的进行 全集分解 P { X + Y ⩽ z , X = 0 } + P { X + Y ⩽ z , X = 2 } = X 和 Y 独立 P { X + Y ⩽ z } \cdotp P { X = 0 } + P { X + Y ⩽ z } \cdotp P { X = 2 } \xlongequal[]{X\text{和}Y\text{独立}}P\{X+Y \leqslant z \}\text{·}P\{X=0\} + P\{X+Y \leqslant z \}\text{·}P\{X=2\} X 和 Y 独立 P { X + Y ⩽ z } \cdotp P { X = 0 } + P { X + Y ⩽ z } \cdotp P { X = 2 } = 将 X 的值代入 1 2 P { Y ⩽ z } + 1 2 P { Y ⩽ z − 2 } \xlongequal[]{\text{将}X\text{的值代入}}\frac{1}{2} P\{Y \leqslant z\} + \frac{1}{2} P\{Y \leqslant z-2\} 将 X 的值代入 2 1 P { Y ⩽ z } + 2 1 P { Y ⩽ z − 2 } 根据小 y 和小 x \text{小}y\text{和小}x 小 y 和小 x z z z F Z ( z ) F_Z(z) F Z ( z ) (法一) 如图所示, z ⩽ 0 z \leqslant 0 z ⩽ 0 F Z ( z ) = 0 + 0 = 0 F_Z(z)=0+0=0 F Z ( z ) = 0 + 0 = 0 当 0 < z ⩽ 1 0<z \leqslant 1 0 < z ⩽ 1 F Z ( z ) = 1 2 ∫ 0 z 2 y d y + 0 = z 2 2 \displaystyle F_Z(z)=\frac{1}{2} \int_0^z 2 y \mathrm{~d} y+0=\frac{z^2}{2} F Z ( z ) = 2 1 ∫ 0 z 2 y d y + 0 = 2 z 2 当 1 < z ⩽ 2 1<z \leqslant 2 1 < z ⩽ 2 F Z ( z ) = 1 2 ∫ 0 1 2 y d y + 0 = 1 2 \displaystyle F_Z(z)=\frac{1}{2} \int_0^1 2 y \mathrm{~d} y+0=\frac{1}{2} F Z ( z ) = 2 1 ∫ 0 1 2 y d y + 0 = 2 1 当 2 < z ⩽ 3 2<z \leqslant 3 2 < z ⩽ 3 F Z ( z ) = 1 2 + 1 2 ∫ 0 z − 2 2 y d y = 1 2 + ( z − 2 ) 2 2 \displaystyle F_Z(z)=\frac{1}{2}+\frac{1}{2} \int_0^{z-2} 2 y \mathrm{~d} y=\frac{1}{2}+\frac{(z-2)^2}{2} F Z ( z ) = 2 1 + 2 1 ∫ 0 z − 2 2 y d y = 2 1 + 2 ( z − 2 ) 2 当 z > 3 z>3 z > 3 F Z ( z ) = 1 F_Z(z)=1 F Z ( z ) = 1 求 Z Z Z f Z ( z ) f_Z(z) f Z ( z ) f Z ( z ) = F Z ′ ( z ) f_Z(z) = F_Z^{\prime}(z) f Z ( z ) = F Z ′ ( z ) f Z ( z ) = { z , 0 < z < 1 , z − 2 , 2 < z < 3 , 0 , 其他. \displaystyle f_Z(z) = \begin{cases}z, & 0<z<1, \\ z-2, & 2<z<3, \\ 0, & \text { 其他. }\end{cases} f Z ( z ) = ⎩ ⎨ ⎧ z , z − 2 , 0 , 0 < z < 1 , 2 < z < 3 , 其他 . (23) (本题满分 11 分)n n n μ \mu μ n n n X 1 , X 2 , ⋯ , X n X_{1}, X_{2}, \cdots, X_{n} X 1 , X 2 , ⋯ , X n N ( μ , σ 2 ) \displaystyle N\left(\mu, \sigma^{2}\right) N ( μ , σ 2 ) n n n Z i = ∣ X i − μ ∣ ( i = 1 , 2 , ⋯ , n ) Z_{i}=\left|X_{i}-\mu\right|(i=1,2, \cdots, n) Z i = ∣ X i − μ ∣ ( i = 1 , 2 , ⋯ , n ) Z 1 , Z 2 , ⋯ , Z n Z_{1}, Z_{2}, \cdots, Z_{n} Z 1 , Z 2 , ⋯ , Z n σ \displaystyle \sigma σ Z 1 Z_{1} Z 1 σ \displaystyle \sigma σ σ \displaystyle \sigma σ
(23) 读题 某工程师为了解一台天平的精度,用该天平对一物体的质量做 n n n μ \mu μ n n n X 1 , X 2 , ⋯ , X n X_{1}, X_{2}, \cdots, X_{n} X 1 , X 2 , ⋯ , X n N ( μ , σ 2 ) \displaystyle N\left(\mu, \sigma^{2}\right) N ( μ , σ 2 ) n n n Z i = ∣ X i − μ ∣ ( i = 1 , 2 , ⋯ , n ) Z_{i}=\left|X_{i}-\mu\right|(i=1,2, \cdots, n) Z i = ∣ X i − μ ∣ ( i = 1 , 2 , ⋯ , n ) Z 1 , Z 2 , ⋯ , Z n Z_{1}, Z_{2}, \cdots, Z_{n} Z 1 , Z 2 , ⋯ , Z n σ \displaystyle \sigma σ Z 1 Z_{1} Z 1 σ \displaystyle \sigma σ σ \displaystyle \sigma σ (1)Z 1 = ∣ X 1 − μ ∣ \displaystyle Z_1=\left|X_1-\mu\right| Z 1 = ∣ X 1 − μ ∣ X 1 − μ ∼ N ( 0 , σ 2 ) \displaystyle X_1-\mu \sim N\left(0, \sigma^2\right) X 1 − μ ∼ N ( 0 , σ 2 ) X 1 − μ σ ∼ N ( 0 , 1 ) \displaystyle \frac{X_1-\mu}{\sigma} \sim N(0,1) σ X 1 − μ ∼ N ( 0 , 1 ) 当 z < 0 z<0 z < 0 F Z 1 ( z ) = 0 F_{Z_1}(z)=0 F Z 1 ( z ) = 0 当 z ⩾ 0 z \geqslant 0 z ⩾ 0 F Z 1 ( z ) = 定义 P { Z 1 ⩽ z } = Z i = ∣ X i − μ ∣ P { ∣ X 1 − μ ∣ ⩽ z } \displaystyle F_{Z_1}(z) \xlongequal[]{\text{定义}}P\left\{Z_1 \leqslant z\right\}\xlongequal[]{Z_{i}=\left|X_{i}-\mu\right|}P\left\{\left|X_1-\mu\right| \leqslant z\right\} F Z 1 ( z ) 定义 P { Z 1 ⩽ z } Z i = ∣ X i − μ ∣ P { ∣ X 1 − μ ∣ ⩽ z } = 标准化 P { ∣ X 1 − μ σ ∣ ⩽ z σ } = 去绝对值 P { − z σ ⩽ X 1 − μ σ ⩽ z σ } \displaystyle \xlongequal[]{\text{标准化}}P\left\{\left|\frac{X_1-\mu}{\sigma}\right| \leqslant \frac{z}{\sigma}\right\}\xlongequal[]{\text{去绝对值}}P\left\{-\frac{z}{\sigma} \leqslant \frac{X_1-\mu}{\sigma} \leqslant \frac{z}{\sigma}\right\} 标准化 P { σ X 1 − μ ⩽ σ z } 去绝对值 P { − σ z ⩽ σ X 1 − μ ⩽ σ z } = Φ ( z σ ) − Φ ( − z σ ) \displaystyle =\Phi\left(\frac{z}{\sigma}\right)-\Phi\left(-\frac{z}{\sigma}\right) = Φ ( σ z ) − Φ ( − σ z ) = 2 Φ ( z σ ) − 1 \displaystyle =2 \Phi\left(\frac{z}{\sigma}\right)-1 = 2Φ ( σ z ) − 1 于是, Z 1 Z_1 Z 1 F Z 1 ( z ) = { 2 Φ ( z σ ) − 1 , z ⩾ 0 , 0 , z < 0. \displaystyle F_{Z_1}(z)= \begin{cases}2 \Phi\left(\frac{z}{\sigma}\right)-1, & z \geqslant 0, \\ 0, & z<0 .\end{cases} F Z 1 ( z ) = { 2Φ ( σ z ) − 1 , 0 , z ⩾ 0 , z < 0. 其中[ Φ ( z σ ) ] ′ = φ ( z σ ) ⋅ 1 σ \displaystyle \left[\Phi\left(\frac{z}{\sigma}\right)\right]^{\prime}=\varphi\left(\frac{z}{\sigma}\right) \cdot \frac{1}{\sigma} [ Φ ( σ z ) ] ′ = φ ( σ z ) ⋅ σ 1 因此, Z 1 Z_1 Z 1 f Z 1 ( z ) = F Z 1 ′ ( z ) = { 2 σ φ ( z σ ) , z ⩾ 0 , 0 , z < 0 \displaystyle f_{Z_1}(z)=F_{Z_1}^{\prime}(z)= \begin{cases}\frac{2}{\sigma} \varphi\left(\frac{z}{\sigma}\right), z \geqslant 0, \\ 0, z<0\end{cases} f Z 1 ( z ) = F Z 1 ′ ( z ) = { σ 2 φ ( σ z ) , z ⩾ 0 , 0 , z < 0 将φ ( z σ ) \displaystyle \varphi(\frac{z}{\sigma}) φ ( σ z ) φ ( x ) = f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 σ = 1 1 2 π e − x 2 2 \displaystyle \varphi(x)\xlongequal[f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}]{\sigma=1}\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} φ ( x ) σ = 1 f ( x ) = 2 π σ 1 e − 2 σ 2 ( x − μ ) 2 2 π 1 e − 2 x 2 { 2 π 1 σ e − z 2 2 σ 2 , z ⩾ 0 , 0 , z < 0 , \displaystyle \begin{cases}\sqrt{\frac{2}{\pi}} \frac{1}{\sigma} \mathrm{e}^{-\frac{z^2}{2 \sigma^2}}, & z \geqslant 0, \\ 0, & z<0,\end{cases} { π 2 σ 1 e − 2 σ 2 z 2 , 0 , z ⩾ 0 , z < 0 , (2) E ( Z 1 ) = ∫ − ∞ + ∞ z f Z 1 ( z ) d z = 代入概率密度 z ∫ 0 + ∞ z ⋅ 2 π ⋅ 1 σ ⋅ e − z 2 2 σ 2 d z \displaystyle E\left(Z_1\right)=\int_{-\infty}^{+\infty} z f_{Z_1}(z) \mathrm{d} z\xlongequal[]{\text{代入概率密度}z}\int_0^{+\infty} z \cdot \sqrt{\frac{2}{\pi}} \cdot \frac{1}{\sigma} \cdot e^{-\frac{z^2}{2 \sigma^2}} d z E ( Z 1 ) = ∫ − ∞ + ∞ z f Z 1 ( z ) d z 代入概率密度 z ∫ 0 + ∞ z ⋅ π 2 ⋅ σ 1 ⋅ e − 2 σ 2 z 2 d z = 凑微分 ∫ 0 + ∞ 2 π ⋅ σ ⋅ e − z 2 2 σ 2 d ( z 2 2 σ 2 ) \displaystyle \xlongequal[]{\text{凑微分}}\int_0^{+\infty} \sqrt{\frac{2}{\pi}} \cdot \sigma \cdot e^{-\frac{z^2}{2 \sigma^2}} d\left(\frac{z^2}{2 \sigma^2}\right) 凑微分 ∫ 0 + ∞ π 2 ⋅ σ ⋅ e − 2 σ 2 z 2 d ( 2 σ 2 z 2 ) = 牛莱 2 π ⋅ σ ⋅ − e − z 2 2 σ 2 ∣ 0 + ∞ \displaystyle \xlongequal[]{\text{牛莱}}\sqrt{\frac{2}{\pi}} \cdot \sigma \cdot-\left.e^{-\frac{z^2}{2 \sigma^2}}\right|_0 ^{+\infty} 牛莱 π 2 ⋅ σ ⋅ − e − 2 σ 2 z 2 0 + ∞ = 0 − ( − 2 π ⋅ σ ) = 2 π ⋅ σ \displaystyle =0-\left(-\sqrt{\frac{2}{\pi}} \cdot \sigma\right)=\sqrt{\frac{2}{\pi}} \cdot \sigma = 0 − ( − π 2 ⋅ σ ) = π 2 ⋅ σ 故 σ = π 2 E ( Z 1 ) \displaystyle \sigma=\sqrt{\frac{\pi}{2}} E\left(Z_1\right) σ = 2 π E ( Z 1 ) Z ˉ \bar{Z} Z ˉ E ( Z 1 ) E\left(Z_1\right) E ( Z 1 ) σ \displaystyle \sigma σ σ ^ = π 2 Z ˉ \displaystyle \hat{\sigma}=\sqrt{\frac{\pi}{2}} \bar{Z} σ ^ = 2 π Z ˉ (3)求最大似然估计 (III) 设 z 1 , z 2 , ⋯ , z n z_1, z_2, \cdots, z_n z 1 , z 2 , ⋯ , z n Z 1 , Z 2 , ⋯ , Z n Z_1, Z_2, \cdots, Z_n Z 1 , Z 2 , ⋯ , Z n f z 1 ( z ) = 2 π ⋅ 1 σ e − z 1 2 2 σ 2 \displaystyle f_{z_1}(z)=\sqrt{\frac{2}{\pi}} \cdot \frac{1}{\sigma} e^{-\frac{z_1^2}{2 \sigma^2}} f z 1 ( z ) = π 2 ⋅ σ 1 e − 2 σ 2 z 1 2 则似然函数为概率密度连乘(三项连乘:系数连乘,σ \displaystyle \sigma σ L ( σ ) = L ( z 1 , z 2 , ⋯ , z n ; σ ) = ∏ i = 1 n f Z i ( z i ) = { ( 2 π ) n 2 1 σ n e − 1 2 σ 2 ( z 1 2 + z 2 2 + ⋯ + z 0 2 ) , , z 1 > 0 , z 2 > 0 , ⋯ , z n > 0 , 0 , 其他. \displaystyle L(\sigma)=L\left(z_1, z_2, \cdots, z_n ; \sigma\right)=\prod_{i=1}^n f_{Z_i}\left(z_i\right)= \begin{cases}\left(\frac{2}{\pi}\right)^{\frac{n}{2}} \frac{1}{\sigma^n} \mathrm{e}^{-\frac{1}{2 \sigma^2\left(z_1^2+z_2^2+\cdots+z_0^2\right)},}, & z_1>0, z_2>0, \cdots, z_n>0, \\ 0, & \text { 其他. }\end{cases} L ( σ ) = L ( z 1 , z 2 , ⋯ , z n ; σ ) = i = 1 ∏ n f Z i ( z i ) = { ( π 2 ) 2 n σ n 1 e − 2 σ 2 ( z 1 2 + z 2 2 + ⋯ + z 0 2 ) 1 , , 0 , z 1 > 0 , z 2 > 0 , ⋯ , z n > 0 , 其他 . 取对数:ln L ( σ ) = n 2 ln 2 π − n ln σ − 1 2 σ 2 ( z 1 2 + z 2 2 + ⋯ + z n 2 ) . \displaystyle \ln L(\sigma)=\frac{n}{2} \ln \frac{2}{\pi}-n \ln \sigma-\frac{1}{2 \sigma^2}\left(z_1^2+z_2^2+\cdots+z_n^2\right) . ln L ( σ ) = 2 n ln π 2 − n ln σ − 2 σ 2 1 ( z 1 2 + z 2 2 + ⋯ + z n 2 ) . 求导:d [ ln L ( σ ) ] d σ = − n σ + 1 σ 3 ( z 1 2 + z 2 2 + ⋯ + z n 2 ) = 0 \displaystyle \frac{\mathrm{d}[\ln L(\sigma)]}{\mathrm{d} \sigma}=-\frac{n}{\sigma}+\frac{1}{\sigma^3}\left(z_1^2+z_2^2+\cdots+z_n^2\right)=0 d σ d [ ln L ( σ )] = − σ n + σ 3 1 ( z 1 2 + z 2 2 + ⋯ + z n 2 ) = 0 解得 σ = 1 n ∑ i = 1 n z i 2 \displaystyle \sigma=\sqrt{\frac{1}{n} \sum_{i=1}^n z_i^2} σ = n 1 i = 1 ∑ n z i 2 因此, σ \displaystyle \sigma σ → 加帽子 σ ^ = 1 n ∑ i = 1 n Z i 2 . \displaystyle \xrightarrow[]{\text{加帽子}}\hat{\sigma}=\sqrt{\frac{1}{n} \sum_{i=1}^n Z_i^2} . 加帽子 σ ^ = n 1 i = 1 ∑ n Z i 2 . 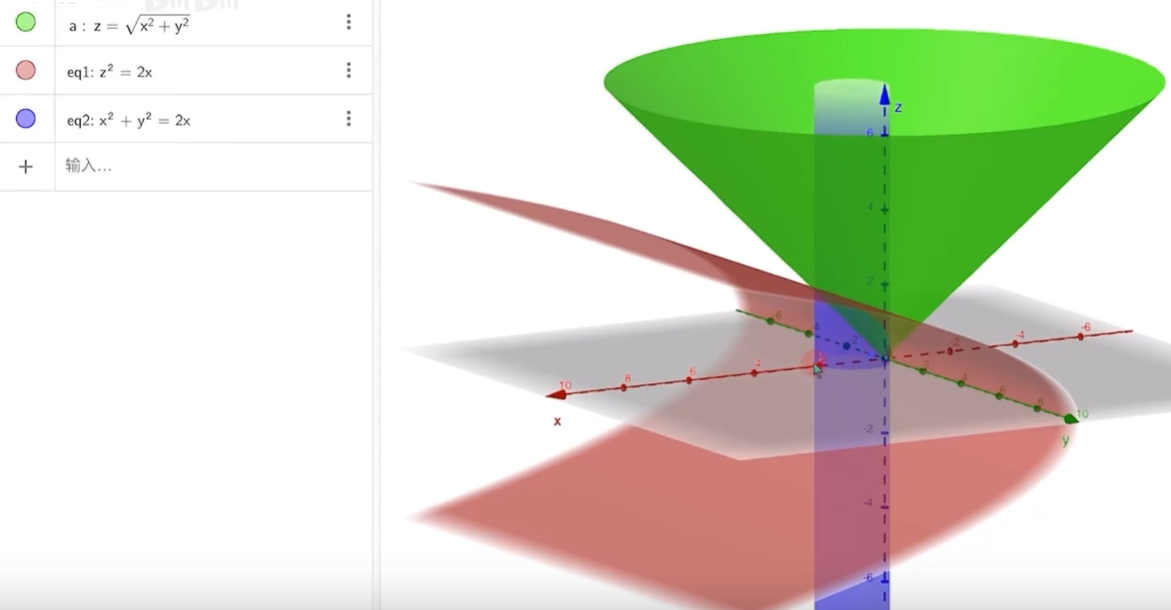
 ,
,